2877. На плоскости даны точки A
и B
. Найдите геометрическое место точек C
, для которых \angle C\gt\angle B
и треугольник ABC
:
а) остроугольный;
б) тупоугольный.
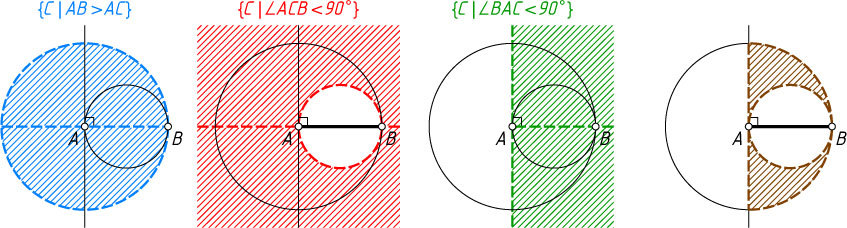
Решение. а) Условие \angle C\gt\angle B
равносильно тому, что AB\gt AC
, поэтому точка C
лежит внутри открытого круга с центром в точке A
и радиуса AB
(см. задачу 1772). В этом случае угол B
не самый большой в треугольнике, поэтому он не может быть тупым. Угол C
острый тогда и только тогда, когда точка C
лежит вне окружности с диаметром AB
. Угол A
острый тогда и только тогда, когда точка C
лежит с той же стороны от перпендикуляра к AB
, проходящего через точку A
, что и точка B
. Ответом является пересечение трёх указанных множеств (см. рис. 1).
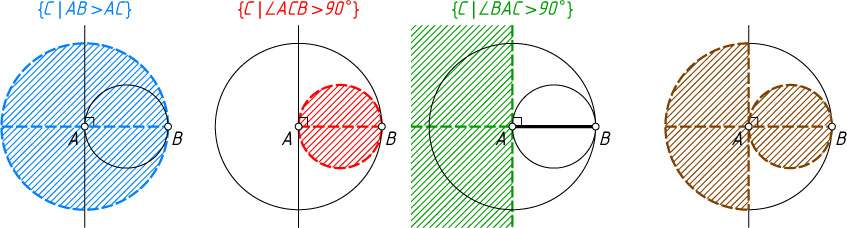
б) Условие \angle C\gt\angle B
равносильно тому, что AB\gt AC
, поэтому точка C
лежит внутри открытого круга с центром в точке A
и радиуса AB
(см. задачу 1772). В этом случае угол B
не самый большой в треугольнике, поэтому он не может быть тупым. Угол C
тупой тогда и только тогда, когда точка C
лежит внутри окружности с диаметром AB
. Угол A
тупой тогда и только тогда, когда точка C
лежит в полуплоскости, граница которой — перпендикуляр к AB
, проходящий через точку A
, не содержащей точку B
. Ответом является пересечение первого из указанных множеств с объединением двух других (см. рис. 2).
Источник: Московская математическая олимпиада. — 1993, LVI, 9 класс
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 1, с. 20

