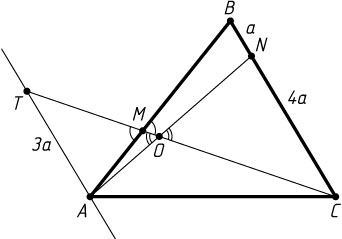
2916. На сторонах AB
и BC
треугольника ABC
расположены точки M
и N
соответственно, причём AM:MB=3:5
, BN:NC=1:4
. Прямые CM
и AN
пересекаются в точке O
. Найдите отношения OA:ON
и OM:OC
.
Ответ. 3:4
; 3:32
.
Указание. Проведите через вершину A
прямую, параллельную стороне BC
, и рассмотрите две пары подобных треугольников (или примените теорему Менелая, см. задачу 1622).
Решение. Первый способ. Через точку A
проведём прямую, параллельную BC
. Пусть T
— точка её пересечения с прямой MC
. Положим BN=a
, CN=4a
.
Из подобия треугольников AMT
и BMC
(коэффициент \frac{3}{5}
) находим, что
AT=\frac{3}{5}BC=\frac{3}{5}(BN+NC)=\frac{3}{5}(a+4a)=3a,
а из подобия треугольников AOT
и NOC
—
\frac{OA}{ON}=\frac{AT}{CN}=\frac{3a}{4a}=\frac{3}{4}.
Аналогично находим, что \frac{OM}{OC}=\frac{3}{32}
.
Второй способ. Через точку N
проведём прямую, параллельную CM
, до пересечения с прямой AB
в точке K
. Тогда MK:KB=CN:NB=4:1
, откуда AO:ON=AM:MK=3:4
. Аналогично находим OM:OC
.
Третий способ. Разместим в точках A
, B
, C
массы 20, 12, 3 соответственно. Тогда центр масс точек A
и B
находится в точке M
, а центр масс точек B
и C
— в точке N
. Следовательно, центр масс точек A
, B
, C
находится на пересечении отрезков CM
и AN
, т. е. в точке O
. Отсюда
OA:ON=(12+3):20=3:4,~OM:OC=3:(12+20)=3:32.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 43
