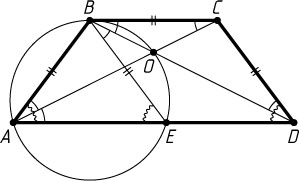
2953. В трапеции ABCD
известно, что AB=BC=CD
. Диагонали трапеции пересекаются в точке O
. Окружность, описанная около треугольника ABO
, пересекает основание AD
в точке E
. Докажите, что BEDC
— ромб.
Решение. Первый способ. Диагонали равнобедренной трапеции образуют равные углы с основанием, поэтому
\angle BDC=\angle DBC=\angle BCA=\angle CAD,
а так как вписанные в окружность углы OAE
и OBE
опираются на одну и ту же дугу, то
\angle CAD=\angle OAE=\angle OBE=\angle DBE.
Таким образом, \angle BDC=\angle DBE
, следовательно, BE\parallel CD
. Тогда четырёхугольник BEDC
— параллелограмм с равными соседними сторонами. Следовательно, BEDC
— ромб.
Второй способ. Из равенства BC=CD
и свойств равнобедренной трапеции следует, что
\angle CBO=\angle CBD=\angle CAB=\angle OAB.
Тогда по теореме, обратной теореме об угле между касательной и хордой (см. задачу 144), BC
— касательная к окружности, описанной около треугольника AOB
. Хорда AE
параллельна этой касательной, значит, треугольник ABE
— равнобедренный, поэтому BE=AB=BC
и \angle BEA=\angle BAE=CDA
. Следовательно, BE\parallel CD
. Тогда четырёхугольник BEDC
— параллелограмм с равными соседними сторонами, т. е. ромб.
Источник: Всероссийская олимпиада школьников. — 2008-2009, XXXV, окружной этап, 9 класс
