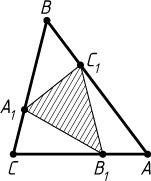
3012. На сторонах AB
, BC
и AC
треугольника ABC
взяты точки C_{1}
, A_{1}
и B_{1}
соответственно, причём
\frac{AC_{1}}{C_{1}B}=\frac{BA_{1}}{A_{1}C}=\frac{CB_{1}}{B_{1}A}=2.
Найдите площадь треугольника A_{1}B_{1}C_{1}
, если площадь треугольника ABC
равна 1.
Ответ. \frac{1}{3}
.
Указание. Треугольники, отсекаемые от данного прямыми A_{1}B_{1}
, B_{1}C_{1}
и A_{1}C_{1}
, — равновелики.
Решение. Заметим, что
S_{\triangle C_{1}BA_{1}}=\frac{BC_{1}}{BA}\cdot\frac{BA_{1}}{BC}\cdot S_{\triangle ABC}=\frac{2}{9}
(см. задачу 3007). Аналогично
S_{\triangle B_{1}CA_{1}}=S_{\triangle B_{1}AC_{1}}=\frac{2}{9}.
Следовательно,
S_{\triangle A_{1}B_{1}C_{1}}=1-3\cdot\frac{2}{9}=\frac{1}{3}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.5, с. 52
