3013. Докажите, что медианы треугольника разбивают его на шесть равновеликих треугольников.
Указание. Медианы треугольника делятся точкой пересечения в отношении 2:1
, считая от вершины.
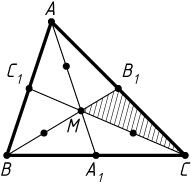
Решение. Пусть M
— точка пересечения медиан AA_{1}
, BB_{1}
, CC_{1}
треугольника ABC
. Тогда
S_{\triangle B_{1}MC}=\frac{1}{3}S_{\triangle B_{1}BC}=\frac{1}{3}\cdot\left(\frac{1}{2}S_{\triangle ABC}\right)=\frac{1}{6}S_{\triangle ABC}.
Аналогично для остальных пяти треугольников.
Примечание. Очевидно, что треугольники AMB
, BMC
и AMC
равновелики. Верно и обратное, если точка M
такова, что треугольники AMB
, BMC
и AMC
равновелики, то M
— точка пересечения медиан треугольника ABC
(см. задачу 3048).
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 2, с. 7
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 2, с. 5
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 5, с. 261
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 50
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 22, с. 99
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.1, с. 81
