3019. Площадь данного выпуклого четырёхугольника равна S
. Найдите площадь четырёхугольника с вершинами в серединах сторон данного.
Ответ. \frac{1}{2}S
.
Указание. Четырёхугольник с вершинами в серединах сторон данного — параллелограмм (см. задачу 1204).
Решение. Первый способ. Пусть d_{1}
и d_{2}
— диагонали данного четырёхугольника, \alpha
— угол между ними. Четырёхугольник с вершинами в серединах сторон данного — параллелограмм (см. задачу 1204) со сторонами \frac{1}{2}d_{1}
и \frac{1}{2}d_{2}
и углом \alpha
между ними. Его площадь равна
\frac{1}{2}d_{1}\cdot\frac{1}{2}d_{2}\sin\alpha=\frac{1}{2}\left(\frac{1}{2}d_{1}d_{2}\sin\alpha\right)=\frac{1}{2}S.
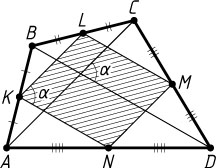
Второй способ. Пусть S
— площадь данного четырёхугольника ABCD
, s
— площадь четырёхугольника, вершины которого — середины K
, L
, M
и N
сторон AB
, BC
, CD
и AD
соответственно.
Поскольку KL
и MN
— средние линии треугольников ABC
и ADC
, то
S_{\triangle KBL}=\frac{1}{4}S_{\triangle ABC},~S_{\triangle MDN}=\frac{1}{4}S_{\triangle ADC}.
Поэтому
S_{\triangle KBL}+S_{\triangle MDN}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{4}S_{\triangle ADC}=\frac{1}{4}(S_{\triangle ABC}+S_{\triangle ADC})=\frac{1}{4}S.
Аналогично
S_{\triangle KAN}+S_{\triangle MCL}=\frac{1}{4}S.
Следовательно,
s=S-S_{\triangle KBL}-S_{\triangle MDN}-S_{\triangle KAN}-S_{\triangle MCL}=S-\frac{1}{4}S-\frac{1}{4}S=\frac{1}{2}S.
