3025. Диагонали выпуклого четырёхугольника равны a
и b
, а отрезки, соединяющие середины противоположных сторон, равны между собой. Найдите площадь четырёхугольника.
Ответ. \frac{ab}{2}
.
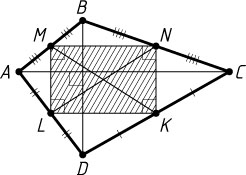
Указание. Середины сторон четырёхугольника являются вершинами параллелограмма (см. задачу 1204).
Решение. Середины сторон любого четырёхугольника являются вершинами параллелограмма (см. задачу 1204). В данном случае этот параллелограмм — прямоугольник, так как его диагонали равны между собой. Диагонали данного четырёхугольника параллельны сторонам этого прямоугольника. Поэтому они взаимно перпендикулярны. Следовательно, если S
— искомая площадь, то S=\frac{1}{2}ab
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1977, вариант 1, № 4
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 32, с. 9
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 40
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.14, с. 24
