3027. Площади треугольников, образованных отрезками диагоналей трапеции и её основаниями, равны S_{1}
и S_{2}
. Найдите площадь трапеции.
Ответ. (\sqrt{S}_{1}+\sqrt{S}_{2})^{2}
.
Указание. Коэффициент подобия указанных треугольников равен \frac{\sqrt{S}_{1}}{\sqrt{S}_{2}}
.
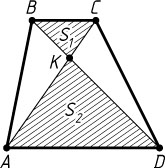
Решение. Пусть K
— точка пересечения диагоналей AC
и BD
трапеции ABCD
и S_{\triangle BKC}=S_{1}
, S_{\triangle AKD}=S_{2}
. Из подобия треугольников BKC
и DKA
следует, что
\frac{CK}{AK}=\frac{\sqrt{S}_{1}}{\sqrt{S}_{2}},
поэтому
S_{\triangle ABK}=\frac{\sqrt{S}_{2}}{\sqrt{S}_{1}}\cdot S_{1}.
Аналогично
S_{\triangle DKC}=\frac{\sqrt{S}_{2}}{\sqrt{S}_{1}}\cdot S_{1}.
Следовательно,
S_{ABCD}=S_{1}+S_{2}+2S_{1}\cdot\frac{\sqrt{S}_{2}}{\sqrt{S}_{1}}=(\sqrt{S}_{1}+\sqrt{S}_{2})^{2}.
Примечание. Верно и обратное: если \sqrt{S_{1}}+\sqrt{S_{2}}=\sqrt{S}
, то четырёхугольник есть трапеция или параллелограмм (см. задачу 5462).
Источник: Саратовская олимпиада. — 1952/1953, I тур, 10 класс
Источник: Андреева А. Н., Барабанов А. И., Чернявский И. Я. Саратовские математические олимпиады. 1950/51—1994/95. — М.: МЦНМО, 2013. — № 18, с. 12
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 11, с. 178
Источник: Вступительный экзамен в МФТИ. — 1959, билет 8, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 59-8-2, с. 72
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 45, с. 45
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.13, с. 53
Источник: Бабинская И. Л. Задачи математических олимпиад. — М.: Наука, 1975. — № 318, с. 36
Источник: Готман Э. Г. Задачи по планиметрии и методы их решения. — М.: Просвещение, 1996. — № 382, с. 109
