3036. Точки P
и Q
расположены на стороне BC
треугольника ABC
, причём BP:PQ:QC=1:2:3
. Точка R
делит сторону AC
этого треугольника так, что \frac{AR}{RC}=\frac{1}{2}
. Чему равно отношение площади четырёхугольника PQST
к площади треугольника ABC
, если S
и T
— точки пересечения прямой BR
с прямыми AQ
и AP
соответственно?
Ответ. 5:24
.
Указание. Найдите отношения \frac{AS}{AQ}
и \frac{AT}{AP}
.
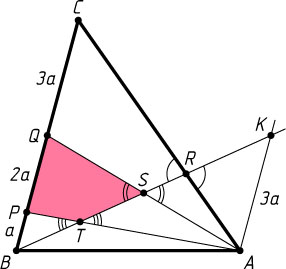
Решение. Обозначим BP=a
. Тогда PQ=2a
, QC=3a
. Проведём через вершину A
прямую, параллельную BC
, и продолжим BR
до пересечения с этой прямой в точке K
. Из подобия треугольников ARK
и CRB
находим, что
AK=\frac{1}{2}BC=3a,
из подобия треугольников ASK
и QSB
—
\frac{AS}{SQ}=\frac{AK}{BQ}=\frac{3a}{3a}=1,
из подобия треугольников ATK
и PTB
—
\frac{AT}{TP}=\frac{AK}{BP}=\frac{3a}{a}=3.
Поэтому
S_{PQST}=S_{\triangle APQ}-S_{\triangle ATS}=S_{\triangle APQ}-\frac{AS}{AQ}\cdot\frac{AT}{AP}\cdot S_{\triangle APQ}=
=S_{\triangle APQ}\left(1-\frac{3}{4}\cdot\frac{1}{2}\right)=\frac{5}{8}S_{\triangle APQ}=\frac{5}{8}\cdot\frac{1}{3}S_{\triangle ABC}=\frac{5}{24}\cdot S_{\triangle ABC}
(см. задачу 3007).
Источник: Вступительный экзамен на биологический факультет МГУ. — 1982, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 55
