3049. Дан выпуклый четырёхугольник площади S
. Внутри него выбирается точка и отображается симметрично относительно середин его сторон. Получаются четыре вершины нового четырёхугольника. Найдите его площадь.
Ответ. 2S
.
Указание. Площадь четырёхугольника с вершинами в серединах сторон данного выпуклого четырёхугольника в два раза меньше площади данного четырёхугольника (см. задачу 3019).
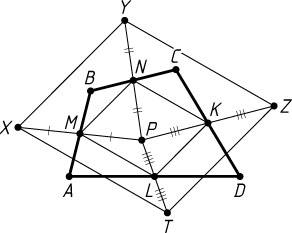
Решение. Пусть M
, N
, K
и L
— середины сторон соответственно AB
, BC
, CD
и AD
четырёхугольника ABCD
, P
— точка внутри этого четырёхугольника; X
, Y
, Z
и T
— образы точки P
при симметрии относительно точек M
, N
, K
и L
соответственно.
Тогда MN
— средняя линия треугольника XPY
. Поэтому
S_{\triangle XPY}=4S_{\triangle MNP}.
Записав аналогичные равенства для треугольников YPZ
, ZPT
и TPX
, получим, что
S_{XYZT}=4(S_{\triangle MNP}+S_{\triangle NKP}+S_{\triangle KLP}+S_{\triangle LMP})=4S_{MNKL},
а так как площадь параллелограмма MNKL
вдвое меньше площади четырёхугольника ABCD
(см. задачу 3019), то
S_{XYZT}=4S_{MNKL}=4\cdot\frac{1}{2}S=2S.
Источник: Московская математическая олимпиада. — 1963, XXVI, 1-й тур, 8 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 7, с. 82
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.39, с. 15
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.16, с. 53
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 12.3, с. 93
