3062. Четырёхугольник разделён диагоналями на четыре треугольника. Площади трёх из них равны 10, 20 и 30, и каждая меньше площади четвёртого треугольника. Найдите площадь данного четырёхугольника.
Ответ. 120.
Указание. Если M
— точка пересечения диагоналей AC
и BD
выпуклого четырёхугольника ABCD
, то \frac{S_{\triangle AMB}}{S_{\triangle AMD}}=\frac{S_{\triangle BMC}}{S_{\triangle DMC}}
(см. задачу 3000).
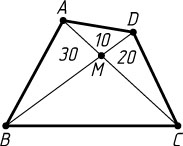
Решение. Пусть M
— точка пересечения диагоналей AC
и BD
четырёхугольника ABCD
. Если
S_{\triangle AMD}=30,~S_{\triangle AMB}=10,~S_{\triangle CMD}=20,
то
\frac{BM}{MD}=\frac{S_{\triangle AMB}}{S_{\triangle AMD}}=\frac{1}{3},
S_{\triangle BMC}=\frac{1}{3}S_{\triangle CMD}=\frac{20}{3}\lt10.
Разбирая остальные возможные случаи, убеждаемся, что возможны только два из них:
S_{\triangle AMB}=20,~S_{\triangle AMD}=10,~S_{\triangle CMD}=30
или
S_{\triangle AMB}=30,~S_{\triangle AMD}=10,~S_{\triangle CMD}=20.
В каждом из возможных случаев S_{\triangle BMC}=60
.
Следовательно, S_{ABCD}=10+20+30+60=120
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. —
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.12, с. 53
