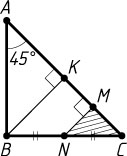
3065. В треугольнике ABC
угол A
равен 45^{\circ}
, а угол C
— острый. Из середины стороны BC
опущен перпендикуляр NM
на сторону AC
. Площади треугольников NMC
и ABC
относятся, как 1:8
. Найдите углы треугольника ABC
.
Ответ. 45^{\circ}
, 90^{\circ}
, 45^{\circ}
.
Указание. \frac{S_{\triangle NMC}}{S_{\triangle ABC}}=\frac{CN}{BC}\cdot\frac{CM}{AC}
(см. задачу 3007).
Решение. Поскольку
\frac{S_{\triangle NMC}}{S_{\triangle ABC}}=\frac{CN}{BC}\cdot\frac{CM}{AC}=\frac{1}{2}\cdot\frac{CM}{AC}=\frac{1}{8}
(см. задачу 3007), то \frac{CM}{AC}=\frac{1}{4}
.
Пусть BK
— высота треугольника ABC
. Тогда NM
— средняя линия треугольника BKC
. Поэтому KM=MC
и AK=KC
, т. е. треугольник ABC
— равнобедренный. Следовательно,
\angle C=45^{\circ},~\angle B=90^{\circ}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1972, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 161
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.22, с. 54
