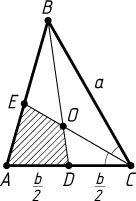
3067. В треугольнике ABC
, площадь которого равна S
, проведены биссектриса CE
и медиана BD
, пересекающиеся в точке O
. Найдите площадь четырёхугольника ADOE
, зная, что BC=a
, AC=b
.
Ответ. \frac{b(3a+b)S}{2(a+b)(2a+b)}
.
Указание. \frac{S_{\triangle BEO}}{S_{\triangle BAD}}=\frac{BE}{BA}\cdot\frac{BO}{BD}.
Решение. По свойству биссектрисы треугольника \frac{BO}{OD}=\frac{BC}{CD}=\frac{2a}{b}
. Поэтому \frac{BO}{BD}=\frac{2a}{2a+b}
. Аналогично \frac{BE}{EA}=\frac{a}{b}
. Поэтому \frac{BE}{AB}=\frac{a}{a+b}
. Тогда (см. задачу 3007)
S_{\triangle BOE}=\frac{BO}{BD}\cdot\frac{BE}{BA}S_{\triangle ABD}=\frac{2a}{2a+b}\cdot\frac{a}{a+b}\cdot\frac{1}{2}S=a^{2}\cdot\frac{S}{(2a+b)(a+b)},
S_{ADOE}=\frac{1}{2}S-\frac{a^{2}S}{(2a+b)(a+b)}=\frac{1}{2}S\left(1-\frac{2a^{2}}{(2a+b)(a+b)}\right)=\frac{b(3a+b)S}{2(2a+b)(a+b)}.
