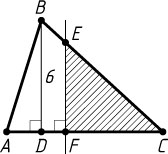
3077. В треугольнике ABC
из точки E
стороны BC
проведена прямая, параллельная высоте BD
и пересекающая сторону AC
в точке F
. Отрезок EF
делит треугольник ABC
на две равновеликие фигуры. Найдите EF
, если BD=6
, \frac{AD}{DC}=\frac{2}{7}
.
Ответ. 9\sqrt{\frac{2}{7}}
.
Указание. \frac{S_{\triangle CEF}}{S_{\triangle CBA}}=\frac{CE}{CB}\cdot\frac{CF}{AC}
(см. задачу 3007).
Решение. Заметим, что
\frac{S_{\triangle CEF}}{S_{\triangle CBA}}=\frac{CE}{CB}\cdot\frac{CF}{AC}=\frac{1}{2}
(см. задачу 3007), а так как AC=\frac{9}{7}CD
, то
\frac{CE}{CB}\cdot\frac{CF}{\frac{9}{7}CD}=\frac{1}{2}.
Отсюда находим, что
\frac{CE}{CB}\cdot\frac{CF}{CD}=\frac{9}{14}.
Из подобия треугольников CEF
и CBD
следует, что \frac{CE}{CB}=\frac{CF}{CD}
. Поэтому
\left(\frac{CE}{CB}\right)^{2}=\frac{9}{14},~\frac{CE}{CB}=\frac{3}{\sqrt{14}},~EF=\frac{BD\cdot CE}{CB}=\frac{6\cdot3}{\sqrt{14}}=\frac{18}{\sqrt{14}}=9\sqrt{\frac{2}{7}}.
Источник: Вступительный экзамен на механико-математический факультет ТбГУ. — 1981
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 87, с. 191
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.23, с. 54
