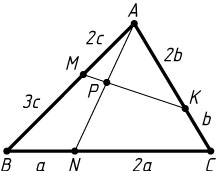
3079. На сторонах AB
, BC
и AC
треугольника ABC
взяты соответственно точки M
, N
и K
так, что AM:MB=2:3
, AK:KC=2:1
, BN:NC=1:2
. В каком отношении прямая MK
делит отрезок AN
?
Ответ. 6:7
, считая от точки A
.
Указание. Пусть P
— точка пересечения прямой MK
с отрезком AN
. Обозначьте \frac{AP}{AN}=x
, и выразите через x
площади треугольников AMP
, AKP
и ABC
.
Решение. Первый способ. Пусть P
— точка пересечения прямой MK
с отрезком AN
. Обозначим \frac{AP}{AN}=x
и S_{\triangle ABC}=S
. Тогда (см. задачу 3007)
S_{\triangle ABN}=\frac{BN}{BC}\cdot S=\frac{1}{3}S,~S_{\triangle ACN}=\frac{CN}{BC}\cdot S=\frac{2}{3}S,
S_{\triangle AMP}=\frac{AM}{AB}\cdot\frac{AP}{AN}\cdot S_{\triangle ABN}=\frac{2}{5}\cdot x\cdot\frac{1}{3}\cdot S=\frac{2}{15}xS,
S_{\triangle AKP}=\frac{AK}{AC}\cdot\frac{AP}{AN}\cdot S_{\triangle ACN}=\frac{2}{3}\cdot x\cdot\frac{2}{3}\cdot S=\frac{4}{9}xS,
S_{\triangle AMK}=\frac{AM}{AB}\cdot\frac{AK}{AC}\cdot S=\frac{2}{5}\cdot\frac{2}{3}\cdot S=\frac{4}{15}S.
Поскольку S_{\triangle AMK}=S_{\triangle AMP}+S_{\triangle AKP}
, то
\frac{2}{15}xS+\frac{4}{9}xS=\frac{4}{15}S.
Отсюда находим, что x=\frac{6}{13}
. Следовательно, \frac{AP}{PN}=\frac{6}{7}
.
Второй способ. Через точку A
проведём прямую l
, параллельную BC
. Пусть E
и F
— точки пересечения прямой MK
с прямыми l
и BC
соответственно. Обозначим CF=t
.
Из подобия треугольников AKE
и CKF
получаем, что AE=2CF=2t
, а из подобия треугольников BMF
и AME
— BF=\frac{3}{2}AE=3t
. Тогда
BC=BF-CF=3t-t=2t,~BN=\frac{1}{3}BC=\frac{2}{3}t,
NF=BF-BN=3t-\frac{2}{3}t=\frac{7}{3}t.
Пусть P
— точка пересечения прямой MK
с отрезком AN
. Из подобия треугольников APE
и NPF
находим, что
\frac{AP}{PN}=\frac{AE}{NF}=\frac{2t}{\frac{7}{3}t}=\frac{6}{7}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 44
