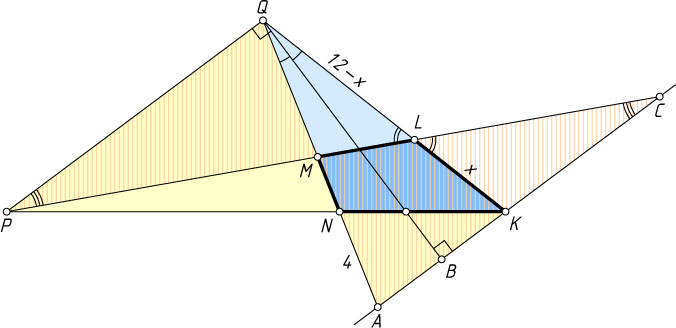
3149. Продолжения сторон KN
и LM
выпуклого четырёхугольника KLMN
пересекаются в точке P
, а продолжения сторон KL
и MN
— в точке Q
. Отрезок PQ
перпендикулярен биссектрисе угла KQN
. Найдите сторону KL
, если KQ=12
, NQ=8
, а площадь четырёхугольника KLMN
равна площади треугольника LQM
.
Ответ. 4.
Указание. Пусть A
— точка пересечения прямой QN
и прямой, проходящей через точку K
параллельно PQ
. Тогда треугольник AQK
— равнобедренный.
Решение. Проведём через точку K
прямую, параллельную PQ
. Пусть A
, B
и C
— точки пересечения этой прямой с прямой QM
, с биссектрисой угла KQN
и с прямой PL
соответственно.
Треугольник AQK
— равнобедренный, так как его биссектриса QB
является высотой. Поэтому QA=QK=12
. Тогда
AN=AQ-QN=12-8=4.
Из подобия треугольников PNQ
и KNA
следует, что
PQ=\frac{AK\cdot QN}{NA}=2AK.
Обозначим KL=x
. Тогда QL=12-x
. Из подобия треугольников KLC
и QLP
следует, что
KC=\frac{PQ\cdot KL}{LQ}=\frac{2AK\cdot x}{12-x}.
Поэтому
AC=AK+KC=AK+\frac{AK\cdot2x}{12-x}=\frac{AK(12+x)}{12-x}.
Из подобия треугольников PMQ
и CMA
следует, что
\frac{QM}{MA}=\frac{PQ}{AC}=\frac{2(12-x)}{12+x}.
Поэтому
\frac{QM}{QA}=\frac{2(12-x)}{24-2x+12+x}=\frac{2(12-x)}{36-x}.
Поскольку S_{\triangle LQM}=S_{LKMN}
, то S_{\triangle LQM}=\frac{1}{2}S_{\triangle KQN}
. Следовательно (см. задачу 3007),
\frac{S_{\triangle LQM}}{S_{\triangle KQN}}=\frac{QM}{QN}\cdot\frac{QL}{QK}=\frac{1}{2},~\mbox{или}~\frac{24(12-x)}{8(36-x)}\cdot\frac{12-x}{12}=\frac{1}{2}.
После упрощения получим квадратное уравнение
x^{2}-8x+24=0.
Условию задачи удовлетворяет только один его корень x=4
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1992, № 5, вариант 4
