3200. Каждая сторона треугольника разделена на три равные части. Точки деления служат вершинами двух треугольников, пересечение которых — шестиугольник. Найдите площадь этого шестиугольника, если площадь данного треугольника равна S
.
Ответ. \frac{2}{9}S
.
Указание. Вершины указанного шестиугольника делят стороны каждого из полученных треугольников на три равные части.
Решение. Пусть ABC
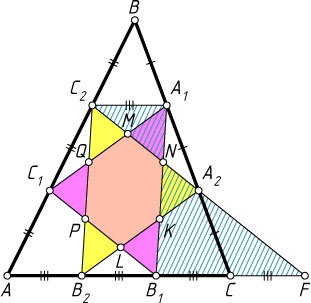
— данный треугольник. Обозначим указанные точки деления, как показано на рисунке. Тогда S_{\triangle A_{1}B_{1}C_{1}}=\frac{1}{3}S
.
Пусть F
— точка пересечения прямых C_{2}A_{2}
и AC
, MNKLPQ
— шестиугольник, о котором говорится в условии задачи. Из равенства треугольников FA_{2}C
и C_{2}A_{2}A_{1}
следует, что
CF=C_{2}A_{1}=\frac{1}{3}AC=CB_{2}.
Из подобия треугольников A_{1}NC_{2}
и B_{1}NF
находим, что
\frac{A_{1}N}{NB_{1}}=\frac{C_{2}A_{1}}{B_{2}F}=\frac{1}{2}.
Аналогично \frac{A_{1}M}{MC_{1}}=\frac{1}{2}
, а так как S_{\triangle A_{1}B_{1}C_{1}}=\frac{1}{3}S_{\triangle ABC}
(см. 3012), то
S_{\triangle A_{1}MN}=\frac{1}{9}S_{\triangle A_{1}B_{1}C_{1}}=\frac{1}{9}\cdot\frac{1}{3}S=\frac{1}{27}S.
Аналогично S_{\triangle B_{1}KL}=S_{\triangle C_{1}PQ}=\frac{1}{27}S
. Следовательно,
S_{MNKLPQ}=\frac{1}{3}S-3\cdot\frac{1}{27}S=\frac{1}{3}S-\frac{1}{9}S=\frac{2}{9}S.
Автор: Золотых А.
Источник: Журнал «Квант». — 1982, № 1, с. 23, М721
Источник: Задачник «Кванта». — 1982, № 1, с. 23, М721
