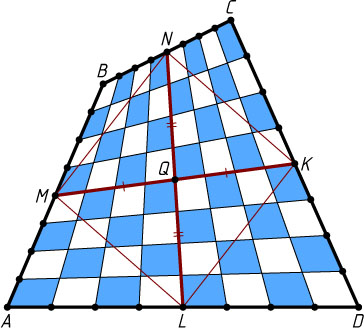
3210. Каждая сторона выпуклого четырёхугольника разделена на 8 равных частей. Соответствующие точки деления на противоположных сторонах соединены друг с другом, и полученные клетки раскрашены в шахматном порядке. Докажите, что сумма площадей синих клеток равна сумме площадей белых клеток.
Указание. Докажите, что каждый из указанных отрезков, соединяющих соответствующие точки деления на противоположных сторонах, делятся на 8 равных частей.
Решение. Пусть M
, N
, K
, L
— середины сторон соответственно AB
, BC
, CD
и AD
выпуклого четырёхугольника ABCD
(рис. 1). Тогда четырёхугольник MNKL
— параллелограмм. Его диагонали MK
и NL
делятся точкой пересечения Q
пополам (см. задачу 1204). Рассуждая аналогично докажем, что каждый из отрезков, соединяющих соответствующие точки деления на противоположных сторонах исходного четырёхугольника, делится на 8 равных частей.
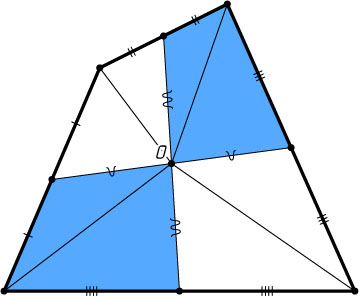
Осталось доказать, что утверждение задачи верно для выпуклого четырёхугольника, все стороны которого разделены пополам (рис. 2). Для этого достаточно заметить, что треугольники с общей вершиной O
и попарно равными основаниями попарно равновелики.
Автор: Произволов В. В.
Источник: Журнал «Квант». — 1980, № 6, с. 18, М626
Источник: Задачник «Кванта». — М626

