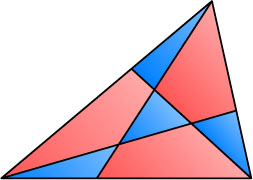
3212. Известно, что четыре синих треугольника на рисунке равновелики.
а) Докажите что три красных четырёхугольника на этом рисунке также равновелики.
б) Найдите площадь одного четырёхугольника, если площадь одного синего треугольника равна 1.
Ответ. 1+\sqrt{5}
.
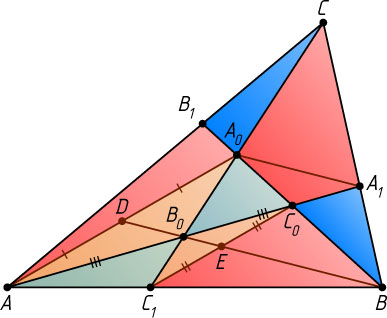
Решение. а) Введём обозначения, как показано на рисунке. Заметим, что треугольники AA_{0}C_{0}
и AA_{0}C_{1}
равновелики (каждый из них составлен из треугольника AA_{0}B_{0}
и одного из синих треугольников). Эти треугольники имеют общее основание AA_{0}
, поэтому их вершины C_{0}
и C_{1}
равноудалены от прямой AA_{0}
, т. е. прямые AA_{0}
и C_{1}C_{0}
параллельны. Аналогично BB_{0}\parallel A_{1}A_{0}
и CC_{0}\parallel B_{1}B_{0}
.
Рассмотрим трапецию AA_{0}C_{0}C_{1}
. Её диагонали пересекаются в точке B_{0}
, а продолжения боковых сторон — в точке B
. Эти точки лежат на прямой, соединяющей середины D
и E
её оснований AA_{0}
и C_{1}C_{0}
(см. задачу 1513), а поскольку эта прямая параллельна A_{1}A_{0}
, точка B_{0}
— середина отрезка A_{1}A
. Поэтому S_{\triangle AB_{0}C}=S_{\triangle B_{0}A_{1}C}
. Следовательно, площади четырёхугольников AB_{0}A_{0}B_{1}
и CA_{0}C_{0}A_{1}
равны. Аналогично докажем, что и третий красный четырёхугольник BC_{0}B_{0}C_{1}
имеет такую же площадь.
б) Чтобы составить уравнение для нахождения искомой площади s
, выразим двумя способами отношение \frac{BC_{1}}{C_{1}A}
:
\frac{BC_{1}}{C_{1}A}=\frac{S_{\triangle CBC_{1}}}{S_{\triangle CC_{1}A}}=\frac{2s+2}{s+2}=\frac{S_{\triangle B_{0}BC_{1}}}{S_{\triangle B_{0}CA_{1}}}=\frac{\frac{s}{2}}{1}=\frac{s}{2}.
Итак, s
удовлетворяет уравнению
s^{2}-2s-4=0,
из которого находим, что s=1+\sqrt{5}
.
Автор: Чиник Б. И.
Источник: Журнал «Квант». — 1983, № 10, с. 43, М827
Источник: Задачник «Кванта». — М827

