3224. Медиана и высота прямоугольного треугольника, проведённые из вершины прямого угла, равны 5 и 4. Найдите катеты.
Ответ. 2\sqrt{5}
, 4\sqrt{5}
.
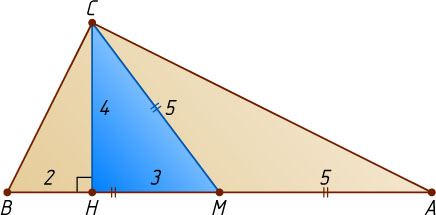
Решение. Пусть CM=5
и CH=4
— медиана и высота прямоугольного треугольника ABC
, проведённые из вершины прямого угла. По теореме Пифагора
MH=\sqrt{CM^{2}-CH^{2}}=\sqrt{25-16}=3.
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), поэтому BM=CM=AM=5
.
Предположим, что AC\gt BC
. Тогда точка H
лежит между точками B
и M
, поэтому
BH=BM-MH=5-3=2,~AH=AM+MH=5+3=8.
Следовательно,
BC=\sqrt{BH\cdot AB}=\sqrt{2\cdot10}=2\sqrt{5},~AC=\sqrt{AH\cdot AB}=\sqrt{8\cdot10}=4\sqrt{5}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 1 из диагностической работы 3
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1, с. 166
