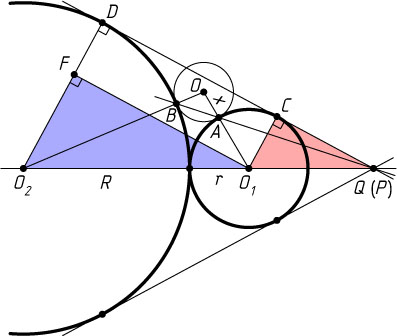
3260. Окружности с центрами O_{1}
и O_{2}
касаются внешним образом. В точках A
и B
их касается внешним образом третья окружность. Докажите, что прямая AB
проходит через точку пересечения общих внешних касательных к первым двум окружностям.
Указание. Докажите, что общая касательная к данным окружностям и прямая AB
пересекают прямую O_{1}O_{2}
в одной и той же точке.
Решение. Пусть r
и R
— радиусы окружностей с центрами O_{1}
и O_{2}
соответственно. Предположим, что r\lt R
. Общие касательные к этим окружностям пересекаются на линии центров, т. е. на прямой O_{1}O_{2}
, в некоторой точке Q
. Пусть прямая AB
пересекает эту прямую в точке P
. Докажем, что O_{1}P=O_{1}Q
. Отсюда будет следовать утверждение задачи.
Пусть прямая, проходящая через точку Q
, касается окружностей с центрами O_{1}
и O_{2}
в точках C
и D
соответственно. Опустим перпендикуляр O_{1}F
на O_{2}D
. Тогда
O_{2}F=O_{2}D-FD=O_{2}D-O_{1}C=R-r.
Прямоугольные треугольники O_{1}CQ
и O_{2}FO_{1}
подобны, поэтому \frac{O_{1}C}{O_{1}Q}=\frac{O_{2}F}{O_{1}O_{2}}
. Следовательно,
O_{1}Q=\frac{O_{1}C\cdot O_{1}O_{2}}{O_{2}F}=\frac{r(R+r)}{R-r}.
Пусть O
— центр третьей окружности, x
— её радиус. Применив теорему Менелая (см. 1622) к треугольнику OO_{1}O_{2}
и прямой AB
, получим, что
\frac{O_{1}P}{PO_{2}}\cdot\frac{O_{2}A}{AO}\cdot\frac{OB}{BO_{1}}=1,~\mbox{или}~\frac{O_{1}P}{O_{1}P+R+r}\cdot\frac{R}{x}\cdot\frac{x}{r}=1.
Значит, \frac{O_{1}P}{O_{1}P+R+r}=\frac{r}{R}
. Отсюда O_{1}P=\frac{r(R+r)}{R-r}=O_{1}Q
. Следовательно, прямые CD
и AB
пересекают линию центров O_{1}O_{2}
в одной и той же точке. Что и требовалось доказать.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 175, с. 90
