3268. Даны две равные пересекающиеся окружности, причём расстояние между центрами больше их радиуса. Докажите, что \beta=3\alpha
(см. рисунок).
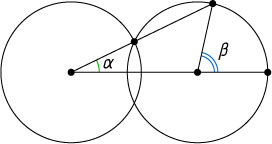
Указание. См. задачу 27.
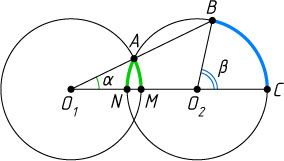
Решение. Пусть A
— точка пересечения равных окружностей с центрами O_{1}
и O_{2}
, продолжение отрезка O_{1}A
пересекает окружность с центром O_{2}
в точке B
, продолжение отрезка O_{1}O_{2}
пересекает эту окружность в точке C
, первая окружность пересекает отрезок O_{1}O_{2}
в точке M
, вторая — в точке N
, \angle BO_{1}C=\alpha
, \angle BO_{2}C=\beta
.
Тогда
\smile AM=\angle AO_{1}M=\alpha,~\smile BC=\angle BO_{2}C=\beta,~\smile AN=\smile AM,
а так как \angle BO_{1}C=\frac{\smile BC-\smile AN}{2}
(см. задачу 27), то \alpha=\frac{\beta-\alpha}{2}
. Отсюда получаем, что \beta=3\alpha
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 12.50, с. 305
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.52, с. 293

