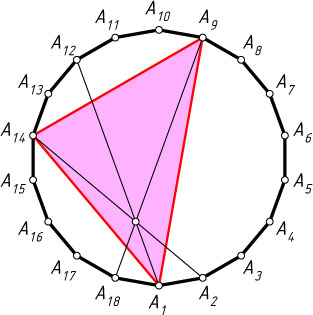
3269. а) Докажите, что диагонали A_{1}A_{12}
, A_{2}A_{14}
и A_{9}A_{18}
правильного восемнадцатиугольника A_{1}\dots A_{18}
пересекаются в одной точке.
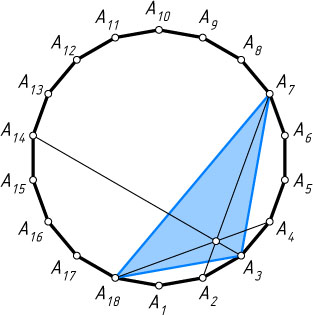
б) Докажите, что диагонали A_{2}A_{7}
, A_{3}A_{14}
и A_{4}A_{18}
правильного восемнадцатиугольника A_{1}\dots A_{18}
пересекаются в одной точке.
Указание. Примените теорему Чевы в тригонометрической форме (см. задачу 1900).
Решение. а) Опишем окружность вокруг правильного восемнадцатиугольника. Градусные меры дуг с концами в соседних вершинах равны \frac{360^{\circ}}{18}=20^{\circ}
, значит,
\angle A_{14}A_{1}A_{12}=\frac{1}{2}\smile A_{12}A_{13}A_{14}=\frac{1}{2}\cdot40^{\circ}=20^{\circ}.
Аналогично находим, что
\angle A_{12}A_{1}A_{9}=30^{\circ},~\angle A_{1}A_{9}A_{18}=10^{\circ},~\angle A_{18}A_{9}A_{14}=40^{\circ},
\angle A_{9}A_{14}A_{2}=70^{\circ},~\angle A_{2}A_{14}A_{1}=10^{\circ}.
Тогда
\frac{\sin\angle A_{14}A_{1}A_{12}}{\sin\angle A_{12}A_{1}A_{9}}\cdot\frac{\sin\angle A_{1}A_{9}A_{18}}{\sin\angle A_{18}A_{9}A_{14}}\cdot\frac{\sin\angle A_{9}A_{14}A_{2}}{\sin\angle A_{2}A_{14}A_{1}}=
=\frac{\sin20^{\circ}}{\sin30^{\circ}}\cdot\frac{\sin10^{\circ}}{\sin40^{\circ}}\cdot\frac{\sin70^{\circ}}{\sin10^{\circ}}=\frac{2\sin20^{\circ}\sin70^{\circ}}{\sin40^{\circ}}=
=\frac{2\sin20^{\circ}\cos20^{\circ}}{\sin40^{\circ}}=\frac{\sin40^{\circ}}{\sin40^{\circ}}=1.
Применяя тригонометрическую форму теоремы Чевы к треугольнику A_{1}A_{9}A_{14}
, получим, что прямые A_{1}A_{12}
, A_{2}A_{14}
и A_{9}A_{18}
пересекаются в одной точке (см. задачу 1900).
б) Рассмотрим треугольник A_{3}A_{7}A_{18}
. Аналогично предыдущему получим, что
\frac{\sin\angle A_{7}A_{18}A_{4}}{\sin\angle A_{4}A_{18}A_{3}}\cdot\frac{\sin\angle A_{18}A_{3}A_{14}}{\sin\angle A_{14}A_{3}A_{7}}\cdot\frac{\sin\angle A_{3}A_{7}A_{2}}{\sin\angle A_{2}A_{7}A_{18}}=
=\frac{\sin30^{\circ}}{\sin10^{\circ}}\cdot\frac{\sin40^{\circ}}{\sin70^{\circ}}\cdot\frac{\sin10^{\circ}}{\sin20^{\circ}}=1.
Следовательно, прямые A_{2}A_{7}
, A_{3}A_{14}
и A_{4}A_{18}
пересекаются в одной точке.
Примечание. См. статью В.Прасолова «Диагонали правильного 18-угольника», Квант, 1995, N5, с.40-42.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 6.59(б), с. 157
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.64(б), с. 158

