3284. В трапеции ABCD
с основаниями AD
и BC
известно, что AB=BC=CD=\frac{1}{2}AD
.
а) Докажите, что AC\perp CD
.
б) Найдите углы трапеции.
Ответ. 60^{\circ}
, 60^{\circ}
, 120^{\circ}
, 120^{\circ}
.
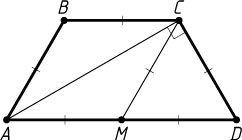
Решение. а) Пусть M
— середина AD
(рис. 1). Тогда AM=\frac{1}{2}AD=BC
и AM\parallel BC
, поэтому четырёхугольник ABCM
— параллелограмм (даже ромб). Значит, CM=AB=\frac{1}{2}AD
. Медиана CM
треугольника ACD
равна половине стороны AD
. Следовательно, \angle ACD=90^{\circ}
(см. задачу 1188).
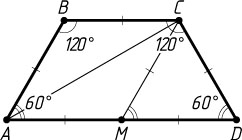
б) Поскольку CD=AB=CM=\frac{1}{2}AD=DM
, треугольник CMD
равносторонний (рис. 2). Следовательно,
\angle ADC=\angle MDC=60^{\circ},~\angle BAD=\angle ADC=60^{\circ},
\angle BCD=\angle ABC=180^{\circ}-\angle BAD=120^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.27, с. 13
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1.27.1, с. 12

