3286. На катетах AC
и BC
прямоугольного треугольника ABC
вне треугольника построены квадраты ACDE
и BFKC
. Точка M
— середина гипотенузы AB
, H
— точка пересечения прямых CM
и DK
.
а) Докажите, что CM\perp DK
.
б) Найдите MH
, если известно, что катеты треугольника ABC
равны 30 и 40.
Ответ. 49.
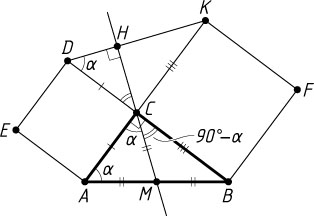
Решение. а) Прямоугольные треугольники DCK
и ACB
равны по двум катетам (рис. 1). Обозначим \angle CDK=\angle CAB=\alpha
. Отрезок CM
— медиана прямоугольного треугольника ABC
, проведённая из вершины прямого угла, поэтому AM=\frac{1}{2}AB=CM
(см. задачу 1109). Значит,
\angle ACM=\angle CAM=\alpha,~\angle DCH=\angle BCM=90^{\circ}-\alpha.
Следовательно,
\angle CHD=180^{\circ}-\angle CDH-\angle DCH=180^{\circ}-\alpha-(90^{\circ}-\alpha)=90^{\circ}.
Что и требовалось доказать.
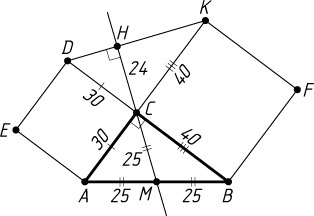
б) Пусть AC=30
, BC=40
(рис. 2). По теореме Пифагора находим, что AB=50
. Тогда CM=\frac{1}{2}AB=25
. Отрезок CH
— высота прямоугольного треугольника DKC
, равного треугольнику ABC
, проведённая из вершины прямого угла, поэтому
CH=\frac{CD\cdot CK}{DK}=\frac{AC\cdot BC}{AB}=\frac{30\cdot40}{50}=24.
Следовательно,
MH=CM+CH=25+24=49.
