3295. Дан параллелограмм ABCD
. Окружности, вписанные в треугольники ABD
и BDC
, касаются диагонали BD
в точках M
и N
соответственно. Окружности, вписанные в треугольники ABC
и ADC
касаются диагонали AC
в точках K
и L
соответственно.
а) Докажите, что MKNL
— прямоугольник.
б) Найдите его площадь, если известно, что BC-AB=4
, а угол между диагоналями параллелограмма ABCD
равен 30^{\circ}
.
Ответ. 4.
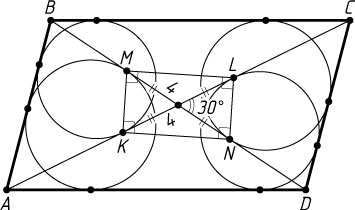
Решение. а) Пусть ABCD
— параллелограмм (рис. 1), в котором AB\lt BC
, M
и N
— точки касания с диагональю BD
вписанных окружностей равных треугольников ABD
и BDC
соответственно, K
и L
— точки касания с диагональю AC
вписанных окружностей равных треугольников ABC
и ADC
соответственно, O
— точка пересечения диагоналей параллелограмма.
Точка O
— центр симметрии параллелограмма, поэтому OM=ON
и OK=OL
, значит, MKNL
— параллелограмм.
Докажем, что MN=KL
. Действительно, для вписанной окружности треугольника ABD
известно, что BM=\frac{AB+BD-AD}{2}
(см. задачу 219), а так как DN=BM
, то
MN=BD-2BM=BD-(AB+BD-AD)=AD-AB.
Аналогично, KL=AD-AB
. Что и требовалось доказать.
Таким образом, диагонали параллелограмма MKNL
равны, следовательно, это прямоугольник.
б) Диагонали прямоугольника MKNL
равны AD-AB=BC-AB=4
(рис. 2), а угол между ними равен 30^{\circ}
, следовательно,
S_{MKNL}=\frac{1}{2}MN\cdot KL\sin30^{\circ}=\frac{1}{2}\cdot16\cdot\frac{1}{2}=4.

Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 3.32, с. 31
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3.32.1, с. 31
Источник: Московская математическая регата. — 2018-2019, третий тур, № 2 (без площади), 8 класс

