3304. Окружности с центрами O_{1}
и O_{2}
касаются внешним образом в точке C
. Прямая касается этих окружностей в различных точках A
и B
соответственно. Найдите угол AO_{2}B
, если известно, что \tg\angle ABC=\frac{1}{2}
.
Ответ. 45^{\circ}
.
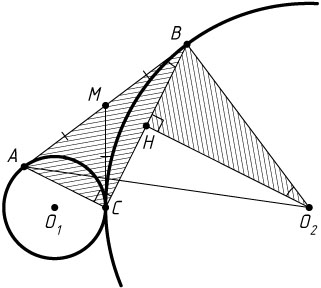
Решение. Пусть M
— точка пересечения отрезка AB
с общей касательной к данным окружностям, проведённой через их точку касания C
. Тогда MA=MC=MB
, значит, \angle ACB=90^{\circ}
(см. задачу 1188).
Опустим перпендикуляр O_{2}H
из центра O_{2}
второй окружности на её хорду BC
. Тогда H
— середина BC
. Из условия задачи следует, что AC=\frac{1}{2}BC=BH
, а так как \angle BO_{2}H=90^{\circ}-\angle O_{2}BH=\angle ABC
, то прямоугольные треугольники BO_{2}H
и ABC
равны по катету и противолежащему острому углу. Значит, O_{2}B=AB
. Следовательно, \angle AO_{2}B=\angle BAO_{2}=45^{\circ}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9, с. 5
