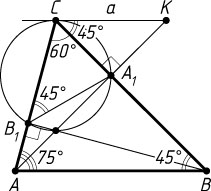
3316. Углы при вершинах A
и B
треугольника ABC
равны 75^{\circ}
и 45^{\circ}
соответственно, AA_{1}
и BB_{1}
— высоты треугольника. Касательная в точке C
к окружности, описанной около треугольника A_{1}B_{1}C
, пересекается с прямой AA_{1}
в точке K
. Известно, что CK=a
. Найдите радиус окружности, описанной около треугольника ABC
.
Ответ. a
.
Указание. Треугольник A_{1}B_{1}C
подобен треугольнику ABC
с коэффициентом \cos\angle ACB=\cos60^{\circ}=\frac{1}{2}
(см. задачу 19).
Решение. Треугольник A_{1}B_{1}C
подобен треугольнику ABC
с коэффициентом \cos\angle ACB=\cos60^{\circ}=\frac{1}{2}
(см. задачу 19), значит, радиус R
описанной окружности треугольника ABC
вдвое больше радиуса r
описанной окружности треугольника A_{1}B_{1}C
.
Из теоремы об угле между касательной и хордой следует, что
\angle KCA_{1}=\angle CB_{1}A_{1}=\angle ABC=45^\circ.
Из прямоугольного треугольника KA_{1}C
находим, что CA_{1}=CK\cos45^{\circ}=\frac{a}{\sqrt{2}}
. По теореме синусов
r=\frac{CA_{1}}{2\sin\angle CB_{1}A_{1}}=\frac{CA_{1}}{2\sin45^{\circ}}=\frac{\frac{a}{\sqrt{2}}}{\frac{2}{\sqrt{2}}}=\frac{a}{2}.
Следовательно, R=2r=a
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 2, задача 6
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6, с. 165
