3317. На сторонах прямоугольного треугольника с катетами a
и b
построены квадраты, лежащие вне треугольника. Найдите площадь треугольника с вершинами в центрах квадратов.
Ответ. \frac{(a+b)^{2}}{4}
.
Решение. Пусть ABC
— данный прямоугольный треугольник с катетами BC=a
, AC=b
и гипотенузой AB
, O_{1}
, O_{2}
и O_{3}
— центры квадратов ABMN
, AKLC
и BCEF
, построенных внешним образом на гипотенузе и катетах AC
и BC
соответственно (рис. 1).
CO_{2}
и CO_{3}
— биссектрисы вертикальных углов, поэтому точки O_{2}
, C
и O_{3}
лежат на одной прямой и
O_{2}O_{3}=CO_{3}+CO_{2}=\frac{a}{\sqrt{2}}+\frac{b}{\sqrt{2}}=\frac{a+b}{\sqrt{2}}.
Пусть P
— проекция точки M
на прямую BC
, R
— проекция точки N
на прямую AC
, а Q
— точка пересечения прямых MP
и NR
. Тогда CPQR
— квадрат со стороной a+b
, его центр совпадает с центром O_{1}
квадрата ABMN
, CO_{1}
— половина диагонали квадрата CPQR
, CO_{1}=\frac{a+b}{\sqrt{2}}
, а так как CO_{1}
— биссектриса прямого угла ACP
(см. задачу 52), то
\angle O_{1}CO_{2}=\angle O_{1}CA+\angle O_{2}CA=45^{\circ}+45^{\circ}=90^{\circ},
т. е. O_{1}C
— высота треугольника O_{1}O_{2}O_{3}
. Следовательно,
S_{\triangle O_{1}O_{2}O_{3}}=\frac{1}{2}O_{2}O_{3}\cdot O_{1}C=\frac{1}{2}\cdot\frac{a+b}{\sqrt{2}}\cdot\frac{a+b}{\sqrt{2}}=\frac{(a+b)^{2}}{4}.
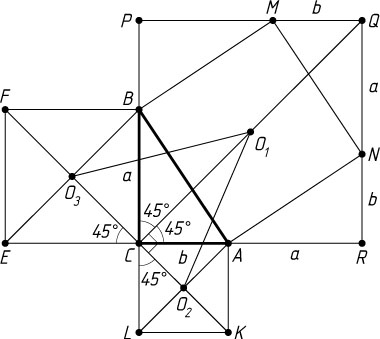
Примечание. То, что центр квадрата CPQR
совпадает с центром квадрата ABMN
следует из более общего утверждения: если вершины одного параллелограмма расположены по одной на сторонах другого, то центры параллелограммов совпадают.
Действительно, пусть вершины X
, Y
, Z
и T
параллелограмма XYZT
расположены соответственно на сторонах AB
, BC
, CD
и AD
параллелограмма ABCD
(рис. 2), а отрезки AC
и YT
пересекаются в точке O
. Из равенства треугольников CYZ
и ATX
(по стороне и двум прилежащим к ней углам) следует, что CY=AT
, значит, треугольники COY
и AOT
также равны по стороне и двум прилежащим к ней углам. Поэтому OY=OT
и AO=OC
, т. е. O
— общая середина диагонали YT
параллелограмма XYZT
(центр этого параллелограмма) и диагонали AC
параллелограмма ABCD
(центр ABCD
). Что и требовалось доказать.
Источник: Вступительный экзамен в МФТИ. — 1965, билет 8, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 65-8-3, с. 111
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 3, задача 6
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6, с. 166
