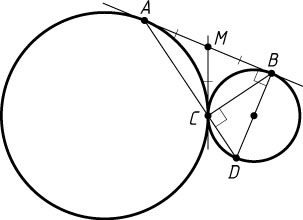
3375. Две окружности касаются внешним образом в точке C
. Прямая касается первой окружности в точке A
, а второй — в точке B
. Прямая AC
пересекает вторую окружность в точке D
, отличной от C
. Найдите BC
, если AC=9
, CD=4
.
Ответ. 6.
Решение. Пусть общая касательная к окружностям, проходящая через точку C
, пересекает отрезок AB
в точке M
. Тогда MA=MC=MB
, т. е. медиана CM
треугольника ABC
равна половине стороны AB
, значит, \angle ACB=90^{\circ}
(см. задачу 1188).
Смежный с углом ACB
угол BCD
также равен 90^{\circ}
, поэтому BD
— диаметр второй окружности, а так как AB
— касательная к этой окружности, то BD\perp AB
.
В прямоугольном треугольнике ABD
отрезок BC
— высота, опущенная на гипотенузу, следовательно,
BC=\sqrt{AC\cdot CD}=\sqrt{9\cdot4}=6.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.30, с. 69
Источник: Вступительный экзамен на механико-математический факультет МГУ. —
