3376. Точка пересечения медиан треугольника ABC
, вершина A
и середины сторон AB
и AC
лежат на одной окружности. Найдите медиану, проведённую из вершины A
, если BC=a
.
Ответ. \frac{a\sqrt{3}}{2}
.
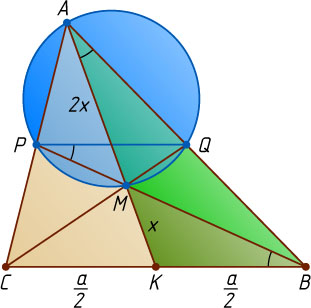
Решение. Первый способ. Пусть K
, P
и Q
— середины сторон BC
, AC
и AB
соответственно, M
— точка пересечения медиан треугольника ABC
(рис. 1).
Обозначим MK=x
. Медианы треугольника точкой пересечения делятся в отношении 2:1
, считая от вершины, поэтому AM=2x
.
Отрезок PQ
— средняя линия треугольника ABC
, поэтому PQ\parallel BC
, значит,
\angle BPQ=\angle CBP=\angle KBM.
Точки A
, P
, M
и Q
лежат на окружности, поэтому
\angle KAB=\angle MAQ=\angle MPQ=\angle BPQ=\angle KBM.
Треугольники KAB
и KBM
подобны по двум углам (угол при вершине K
— общий), значит, \frac{BK}{KM}=\frac{AK}{BK}
, или \frac{\frac{a}{2}}{x}=\frac{3x}{\frac{a}{2}}
, откуда находим, что x=\frac{a}{2\sqrt{3}}
. Следовательно,
AK=3x=3\cdot\frac{a}{2\sqrt{3}}=\frac{a\sqrt{3}}{2}.
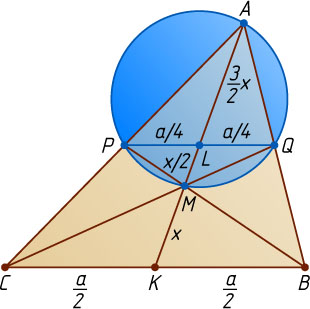
Второй способ (решение Е. Б. Фёдорова). Пусть L
— точка пересечения средней линии PQ
и медианы AK
, M
— точка пересечения медиан треугольника ABC
(рис. 2). Положим MK=x
, AM=2x
. Точка L
— середина AK
, значит,
AL=\frac{3}{2}x,~LM=AM-AL=2x-\frac{3}{2}x=\frac{1}{2}x.
Точка L
является также серединой PQ
, поэтому QL=PL=\frac{1}{4}a
.
Поскольку произведения отрезков пересекающихся хорд окружности равны, PL\cdot QL=AL\cdot LM
, или \frac{a}{4}\cdot\frac{a}{4}=\frac{3}{2}x\cdot\frac{1}{2}x
, откуда находим, что x=\frac{a}{2\sqrt{3}}
. Следовательно,
AK=3x=\frac{3a}{2\sqrt{3}}=\frac{a\sqrt{3}}{2}.
Примечание. Верно и обратное. Если AK=\frac{a\sqrt{3}}{2}
, то точка пересечения медиан треугольника ABC
, вершина A
и середины сторон AB
и AC
лежат на одной окружности (см. задачу 16245).
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.254
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.21, с. 112

