3382. Окружность, построенная как на диаметре на меньшей боковой стороне прямоугольной трапеции, касается большей боковой стороны, равной a
. Найдите среднюю линию трапеции.
Ответ. \frac{a}{2}
.
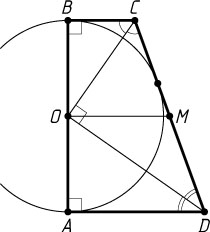
Решение. Пусть центр O
окружности лежит на меньшей боковой стороне AB
прямоугольной трапеции ABCD
, M
— середина большей боковой стороны CD
.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому CO
и DO
— биссектрисы углов BCD
и ADC
, сумма которых равна 180^{\circ}
, значит,
\angle COD=180^{\circ}-(\angle OCD+\angle ODC)=180^{\circ}-\frac{1}{2}(\angle BCD+\angle ADC)=180^{\circ}-\frac{1}{2}\cdot180^{\circ}=90^{\circ}.
Средняя линия OM
трапеции ABCD
— это медиана прямоугольного треугольника COD
, проведённая из вершины прямого угла, следовательно (см. задачу 1109),
OM=\frac{1}{2}CD=\frac{1}{2}a.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 2 из диагностической работы 6.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2, с. 169
