3384. Через середину боковой стороны равнобедренного треугольника со сторонами 12, 18, 18 проведена прямая, разбивающая треугольник на части, площади которых относятся как 1:2
. Найдите длину отрезка этой прямой, заключённого внутри треугольника.
Ответ. \sqrt{97}
или \sqrt{57}
.
Решение. Пусть AB=AC=18
— боковые стороны равнобедренного треугольника ABC
с основанием BC=12
, M
— середина AB
. Обозначим \angle BAC=\alpha
, \angle ABC=\beta
. По теореме косинусов
\cos\alpha=\frac{18^{2}+18^{2}-12^{2}}{2\cdot18\cdot18}=\frac{7}{9}.
Если D
— середина основания BC
, то
\cos\beta=\frac{BD}{AB}=\frac{6}{18}=\frac{1}{3}.
Прямая, о которой говорится в условии задачи, отсекает от данного треугольника треугольник, площадь которого равна третьей части площади треугольника ABC
. При этом либо точка N
лежит либо на боковой стороне AC
(рис. 1), либо на основании BC
(рис. 2).
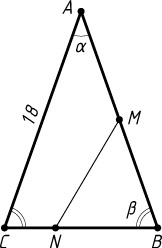
В первом из этих случаев
\frac{S_{\triangle MAN}}{S_{\triangle ABC}}=\frac{AM}{AB}\cdot\frac{AN}{AC}=\frac{1}{3}
(см. задачу 3007), значит,
\frac{AN}{AC}=\frac{1}{3}\cdot\frac{AB}{AM}=\frac{1}{3}\cdot2=\frac{2}{3},
поэтому AN=\frac{2}{3}AC=\frac{2}{3}\cdot18=12
. По теореме косинусов
MN=\sqrt{AM^{2}+AN^{2}-2AM\cdot AN\cos\alpha}=\sqrt{9^{2}+12^{2}-2\cdot9\cdot12\cdot\frac{7}{9}}=\sqrt{57}.
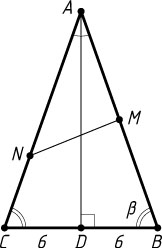
Во втором случае
\frac{S_{\triangle MBN}}{S_{\triangle ABC}}=\frac{BM}{AB}\cdot\frac{BN}{BC}=\frac{1}{3},
значит,
\frac{BN}{BC}=\frac{1}{3}\cdot\frac{AB}{BM}=\frac{1}{3}\cdot2=\frac{2}{3},
поэтому BN=\frac{2}{3}BC=\frac{2}{3}\cdot12=8
. По теореме косинусов
MN=\sqrt{BM^{2}+BN^{2}-2BM\cdot BN\cos\beta}=\sqrt{9^{2}+8^{2}-2\cdot9\cdot8\cdot\frac{1}{3}}=\sqrt{97}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 4 из диагностической работы 4.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4, с. 167

