3386. Окружность S
с центром в вершине прямого угла прямоугольного треугольника касается окружности, вписанной в этот треугольник. Найдите радиус окружности S
, если известно, что катеты треугольника равны 5 и 12.
Ответ. 2(\sqrt{2}\pm1)
.
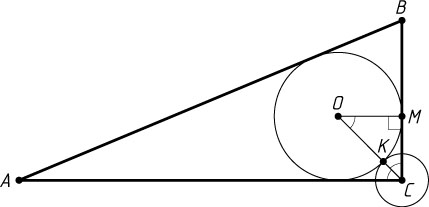
Решение. Пусть окружность S
с центром в вершине C
прямого угла прямоугольного треугольника ABC
с катетами AC=12
, BC=5
и гипотенузой AB=13
в точке K
касается внешним образом вписанной окружности этого треугольника (рис. 1).
Пусть O
— центр вписанной окружности данного треугольника, M
— точка касания вписанной окружности треугольника с катетом BC
. Тогда
OM=\frac{1}{2}(AC+BC-AB)=\frac{1}{2}(12+5-13)=2
(см. задачу 217). Линия центров касающихся окружностей проходит через точку их касания, поэтому OC=CK+OK
, \angle OCM=45^{\circ}
, так как CO
— биссектриса угла ACB
. Из прямоугольного треугольника OCM
находим, что OC=\sqrt{2}OM=2\sqrt{2}
, а так как OK=OM
, то 2\sqrt{2}=2+CK
. Следовательно, CK=2\sqrt{2}-2
, т. е. радиус окружности S
равен 2\sqrt{2}-2
.
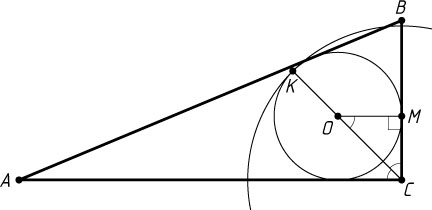
Если окружность S
касается вписанной окружности данного треугольника внутренним образом (рис. 2), то аналогично найдём, что радиус окружности S
равен 2\sqrt{2}+2
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 2 из диагностической работы 4.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2, с. 167

