3387. На сторонах AB
, BC
и AC
треугольника ABC
, площадь которого равна 75, расположены точки M
, N
и K
соответственно. Известно, что M
— середина AB
, площадь треугольника BMN
равна 15, а площадь треугольника AMK
равна 25. Найдите площадь треугольника CNK
.
Ответ. 15.
Решение. Обозначим S_{\triangle ABC}=S
. Тогда (см. задачу 3007)
\frac{S_{\triangle AMK}}{S}=\frac{AM}{AB}\cdot\frac{AK}{AC}=\frac{1}{2}\cdot\frac{AK}{AC},
а так как по условию задачи \frac{S_{AMK}}{S}=\frac{25}{75}=\frac{1}{3}
, то \frac{1}{2}\cdot\frac{AK}{AC}=\frac{1}{3}
, откуда находим, что \frac{AK}{AC}=\frac{2}{3}
, а \frac{CK}{AC}=\frac{1}{3}
. Аналогично находим, что \frac{CN}{BC}=\frac{3}{5}
. Следовательно,
S_{\triangle CNK}=\frac{CK}{AC}\cdot\frac{CN}{BC}\cdot S=\frac{1}{3}\cdot\frac{3}{5}\cdot75=15.
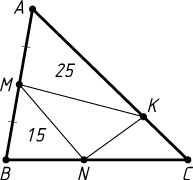
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 1 из диагностической работы 4.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1, с. 167
