3388. В треугольник ABC
со сторонами AB=18
и BC=12
вписан параллелограмм BKLM
, причём точки K
, L
и M
лежат на сторонах AB
, AC
и BC
соответственно. Известно, что площадь параллелограмма составляет \frac{4}{9}
площади треугольника ABC
. Найдите стороны параллелограмма.
Ответ. 8, 6 или 4, 12.
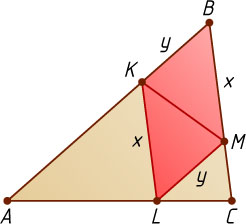
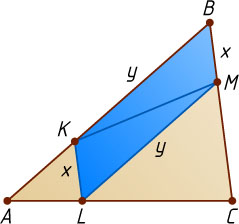
Решение. Обозначим BM=KL=x
, BK=LM=y
, S_{\triangle ABC}=S
. Тогда
S_{BKLM}=\frac{4}{9}S,~S_{\triangle BKM}=\frac{1}{2}S_{BKLM}=\frac{1}{2}\cdot\frac{4}{9}S=\frac{2}{9}S,
а так как
\frac{2}{9}S=S_{\triangle BKM}=\frac{BM}{BC}\cdot\frac{BK}{AB}\cdot S_{\triangle ABC}=\frac{x}{12}\cdot\frac{y}{18}\cdot S
(см. задачу 3007), то xy=48
.
Треугольник AKL
подобен треугольнику ABC
, поэтому \frac{KL}{BC}=\frac{AK}{AB}
, или \frac{x}{12}=\frac{18-y}{18}
, откуда 3x+2y=36
. Из системы \syst{xy=48\\3x+2y=36\\}
находим, что x=8
, y=6
или x=4
, y=12
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Задача 3 из диагностической работы 3.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3, с. 166

