3395. Найдите радиусы описанной, вписанной и вневписанных окружностей треугольника со сторонами 13, 14, 15.
Ответ. \frac{65}{8}
, 4
, 14, 12, \frac{21}{2}
.
Указание. См. задачу 392.
Решение. Пусть стороны AB
, AC
и BC
треугольника ABC
равны 13, 14 и 15 соответственно (рис. 1), R
и r
— радиусы соответственно описанной и вписанной окружностей, r_{a}
, r_{b}
и r_{c}
— радиусы вневписанных окружностей, касающихся сторон BC
, AC
и AB
— соответственно, S
— площадь треугольника ABC
, p
— полупериметр.
По теореме косинусов
\cos\angle BAC=\frac{AB^{2}+AC^{2}-BC^{2}}{2AB\cdot AC}=\frac{169+196-225}{2\cdot13\cdot14}=\frac{5}{13}.
Тогда
\sin\angle BAC=\sqrt{1-\left(\frac{5}{13}\right)^{2}}=\frac{12}{13},
S=\frac{1}{2}AB\cdot AC\sin\angle BAC=\frac{1}{2}\cdot13\cdot14\cdot\frac{12}{13}=84.
Следовательно,
r=\frac{S}{p}=\frac{84}{21}=4.
По теореме синусов
R=\frac{BC}{2\sin\angle BAC}=\frac{15}{2\cdot\frac{12}{13}}=\frac{65}{8}.
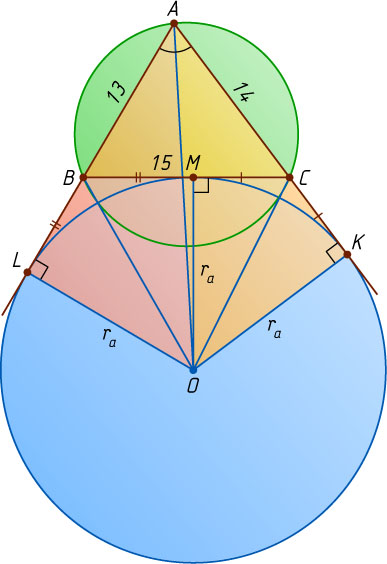
Пусть O
— центр вневписанной окружности, касающейся стороны BC
в точке M
и продолжения сторон AC
и AB
— в точках K
и L
соответственно (рис. 2). Тогда
AK=AL,~CK=CM,~BL=BM,~2p=AC+BC+AB=AC+(CM+BM)+AL=
=(AC+CM)+(AB+BM)=(AC+CK)+(AB+BL)=AK+AB,
значит, AK=AL=p
, поэтому
S=S_{\triangle AOK}+S_{\triangle AOL}-S_{KCBLO}=S_{\triangle AOK}+S_{\triangle AOL}-2S_{BOC}=
=\frac{1}{2}AK\cdot OK+\frac{1}{2}AL\cdot OL-2\cdot\frac{1}{2}BC\cdot OM=\frac{1}{2}pr_{a}+\frac{1}{2}pr_{a}-BC\cdot r_{a}=(p-BC)r_{a}.
Следовательно,
r_{a}=\frac{S}{p-BC}=\frac{84}{21-15}=\frac{84}{6}=14.
Аналогично найдём, что
r_{b}=\frac{S}{p-AC}=\frac{84}{21-14}=\frac{84}{7}=12,~r_{c}=\frac{S}{p-AB}=\frac{84}{21-13}=\frac{84}{8}=\frac{21}{2}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.7, с. 86
