3398. Отрезок, соединяющий середины оснований трапеции, равен 3. Углы при большем основании равны 30^{\circ}
и 60^{\circ}
. Найдите высоту.
Ответ. \frac{3\sqrt{3}}{2}
.
Указание. Через середину меньшего основания трапеции проведите прямые, параллельные боковым сторонам.
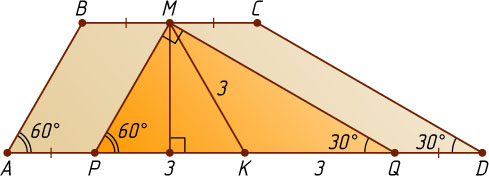
Решение. Через середину M
меньшего основания BC
трапеции ABCD
проведём прямую, параллельную боковой стороне AB
, до пересечения с основанием AD
в точке P
и прямую, параллельную боковой стороне CD
, до пересечения с прямой AD
в точке Q
. Если K
— середина AD
, то
PK=AK-AP=AK-BM=DK-MC=DK-QD=KQ.
Поэтому MK
— медиана треугольника PMQ
, а так как
\angle PMQ=180^{\circ}-60^{\circ}-30^{\circ}=90^{\circ},
то PK=KQ=MK=3
(см. задачу 1109).
Если \angle A=60^{\circ}
, то \angle MPK=60^{\circ}
. Поэтому треугольник PMK
— равносторонний, его высота равна \frac{3\sqrt{3}}{2}
. Следовательно, высота трапеции равна \frac{3\sqrt{3}}{2}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.27, с. 32
