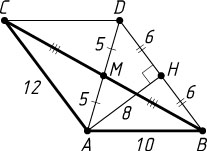
3428. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей стороне, равна 5. Найдите третью сторону и площадь треугольника.
Ответ. 2\sqrt{97}
; 48.
Решение. Пусть AM=5
— медиана треугольника ABC
со сторонами AB=10
, AC=12
. На продолжении AM
за точку M
отложим отрезок MD=AM=5
. Тогда ABDC
— параллелограмм со сторонами CD=AB=10
, BD=AC=12
и диагоналями BC
и AD=10
. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, т. е. BC^{2}+AD^{2}=2AB^{2}+2AC^{2}
(см. задачу 4011). Значит,
BC^{2}=2AB^{2}+2AC^{2}-AD^{2}=2\cdot100+2\cdot144-100=388.
Следовательно, BC=\sqrt{388}=2\sqrt{97}
.
Поскольку AD=10=AB
, треугольник ABD
равнобедренный. Его высота AH
является медианой, поэтому
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{100-36}=8.
Следовательно,
S_{\triangle ABC}=S_{\triangle ABD}=\frac{1}{2}BD\cdot AH=\frac{1}{2}\cdot12\cdot8=48.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 2.17, с. 21
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2.17.1, с. 20
