3435. Точки L
и N
— середины оснований соответственно BC
и AD
трапеции ABCD
, а точки K
и M
— середины диагоналей AC
и BD
соответственно. Известно, что KM=LN
.
а) Докажите, что сумма углов при одном из оснований трапеции равна 90^{\circ}
.
б) Найдите высоту трапеции, если известно, что площадь четырёхугольника KLMN
равна 12, а разность оснований трапеции равна 10.
Ответ. 4,8.
Указание. См. задачу 1204.
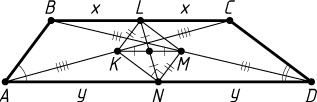
Решение. а) Предположим, что BC\lt AD
(рис. 1). Отрезки KL
и MN
— средние линии треугольников ABC
и ABD
, поэтому KL=MN
и KL\parallel MN
. Значит, KLMN
— параллелограмм, а так как его диагонали KM
и LN
равны, то это прямоугольник. Поскольку AB\parallel KL
, CD\parallel LM
и KL\perp LM
, то AB\perp CD
. Следовательно, \angle BAD+\angle CDA=90^{\circ}
.
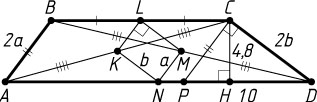
б) Через вершину C
проведём прямую, параллельную AB
(рис. 2). Пусть эта прямая пересекает основание AD
в точке P
. Четырёхугольник ABCP
— параллелограмм, поэтому AP=BC
. Тогда DP=AD-AP=AD-BC=10
. Поскольку AB\perp CD
, то CP\perp CD
. Значит, треугольник DCP
прямоугольный.
Пусть CH
— высота трапеции. Тогда CH
— высота прямоугольного треугольника DCP
, проведённая из вершины прямого угла. Следовательно,
CH=\frac{CD\cdot CP}{PD}=\frac{CD\cdot AB}{PD}=\frac{2LM\cdot2KL}{PD}=4\cdot\frac{LM\cdot KL}{PD}=
=4\cdot\frac{S_{KLMN}}{PD}=4\cdot\frac{12}{10}=4{,}8.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.44, с. 40
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.44.1, с. 40

