3438. Диагональ AC
прямоугольника ABCD
с центром O
образует со стороной AB
угол 30^{\circ}
. Точка E
лежит вне прямоугольника, причём \angle BEC=120^{\circ}
.
а) Докажите, что \angle CBE=\angle COE
.
б) Прямая OE
пересекает сторону AD
прямоугольника в точке K
. Найдите EK
, если известно, что BE=40
и CE=24
.
Ответ. 113.
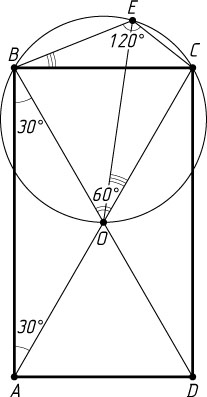
Решение. а) По теореме о внешнем угле треугольника \angle BOC=2\angle BAO=2\cdot30^{\circ}=60^{\circ}
(рис. 1). Поэтому
\angle BEC+\angle BOC=120^{\circ}+60^{\circ}=180^{\circ}.
Значит, точки B
, E
, C
и O
лежат на одной окружности. Вписанные в эту окружность углы CBE
и COE
опираются на одну и ту же дугу, следовательно, \angle CBE=\angle COE
.
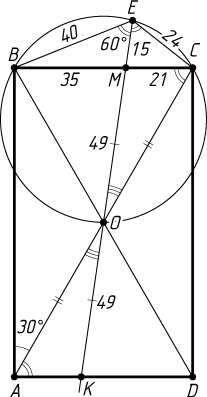
б) По теореме косинусов (рис. 2)
BC=\sqrt{BE^{2}+CE^{2}-2BE\cdot CE\cos120^{\circ}}=
=\sqrt{40^{2}+24^{2}-2\cdot40\cdot24\cdot\left(-\frac{1}{2}\right)}=8\sqrt{25+9+15}=8\cdot7=56.
Вписанные углы BEO
и CEO
опираются на равные хорды BO
и CO
, значит, EO
— биссектриса угла BEC
. Пусть M
— точка её пересечения со стороной BC
. По формуле для биссектрисы треугольника (см. задачу 4021)
EM=\frac{2BE\cdot CE\cos\frac{1}{2}\angle BEC}{BE+CE}=\frac{2\cdot40\cdot24\cos60^{\circ}}{40+24}=15.
По свойству биссектрисы треугольника \frac{CM}{BM}=\frac{CE}{BE}=\frac{24}{40}=\frac{3}{5}
, значит, CM=\frac{3}{8}BC=\frac{3}{8}\cdot56=21
, BM=35
.
По теореме о произведении пересекающихся хорд EM\cdot MO=BM\cdot CM
, откуда находим, что MO=\frac{BM\cdot CM}{EM}=\frac{35\cdot21}{15}=49
. Треугольники COM
и AOK
равны по стороне и двум прилежащим к ней углам, поэтому OK=OM
. Следовательно,
EK=EM+2OM=15+98=113.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 5.29, с. 50
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.29.1, с. 51

