3443. На сторонах AD
и BC
параллелограмма ABCD
взяты соответственно точки M
и N
, причём M
— середина AD
, а BN:NC=1:3
.
а) Докажите, что прямые AN
и AC
делят отрезок BM
на три равные части.
б) Найдите площадь четырёхугольника, образованного пересечениями прямых AN
, AC
, BD
и BC
, если площадь параллелограмма ABCD
равна 40.
Ответ. 9.
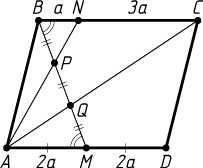
Решение. а) Пусть отрезок BM
пересекает отрезки AN
и AC
в точках P
и Q
соответственно (рис. 1). Положим BN=a
, NC=3a
. Тогда AD=BC=4a
, AM=MD=2a
. Треугольники BPN
и MPA
подобны с коэффициентом \frac{BN}{AM}=\frac{a}{2a}=\frac{1}{2}
, поэтому BP=\frac{1}{3}BM
.
Треугольники AQM
и CQB
подобны с коэффициентом \frac{AM}{BC}=\frac{2a}{4a}=\frac{1}{2}
, поэтому QM=\frac{1}{3}BM
. Значит,
PQ=BM-BP-QM=BM-\frac{1}{3}BM-\frac{1}{3}BM=\frac{1}{3}BM.
Следовательно, BP=PQ=QM
.
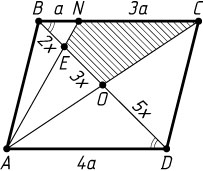
б) Пусть O
— центр параллелограмма, E
— точка пересечения диагонали BD
с отрезком AN
(рис. 2). Требуется найти площадь четырёхугольника COEN
.
Треугольник BEN
подобен треугольнику DEA
с коэффициентом \frac{BN}{AD}=\frac{a}{4a}=\frac{1}{4}
, поэтому \frac{BE}{ED}=\frac{1}{4}
. Тогда \frac{BE}{BD}=\frac{1}{5}
, а \frac{BE}{BO}=\frac{2}{5}
. Значит (см. задачу 3007),
\frac{S_{\triangle BEN}}{S_{\triangle BOC}}=\frac{BE}{BO}\cdot\frac{BN}{BC}=\frac{2}{5}\cdot\frac{1}{4}=\frac{1}{10}.
Следовательно,
S_{COEN}=S_{\triangle BOC}-S_{\triangle BEN}=S_{\triangle BOC}-\frac{1}{10}S_{\triangle BOC}=
=\frac{9}{10}S_{\triangle BOC}=\frac{9}{10}\cdot\frac{1}{4}S_{ABCD}=\frac{9}{40}\cdot40=9.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.27, с. 58
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.28.1, с. 61

