3445. Точки B_{1}
и C_{1}
лежат на сторонах соответственно AC
и AB
треугольника ABC
, причём AB_{1}:B_{1}C=AC_{1}:C_{1}B
. Прямые BB_{1}
и CC_{1}
пересекаются в точке O
.
а) Докажите, что прямая AO
делит пополам сторону BC
.
б) Найдите отношение площади четырёхугольника AB_{1}OC_{1}
к площади треугольника ABC
, если известно, что AB_{1}:B_{1}C=AC_{1}:C_{1}B=1:2
.
Ответ. 1:6
.
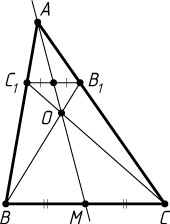
Решение. а) Точки B_{1}
и C_{1}
делят стороны AC
и AB
треугольника ABC
в одном и том же отношении, поэтому B_{1}C_{1}\parallel BC
(рис. 1). Значит, BC_{1}B_{1}C
— трапеция. По замечательному свойству трапеции (см. 1513) прямая AO
проходит через середину M
стороны BC
.
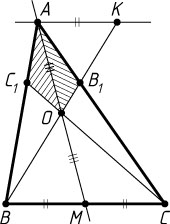
б) Через точку A
проведём прямую, параллельную BC
(рис. 2). Пусть эта прямая пересекает продолжение отрезка BB_{1}
в точке K
. Коэффициент подобия треугольников AB_{1}K
и CB_{1}B
равен \frac{1}{2}
, поэтому AK=\frac{1}{2}BC=BM
. Значит, треугольники AOK
и MOB
равны по стороне и двум прилежащим к ней углам. Тогда O
— середина отрезка AM
.
Пусть площадь треугольника ABC
равна S
. Тогда
S_{\triangle ACM}=\frac{1}{2}S,~S_{\triangle AOC}=\frac{1}{2}S_{\triangle ACM}=\frac{1}{4}S,
S_{\triangle AOB_{1}}=\frac{AB_{1}}{AC}\cdot S_{\triangle AOC}=\frac{1}{3}S_{\triangle AOC}=\frac{1}{3}\cdot\frac{1}{4}S=\frac{1}{12}S.
Аналогично S_{\triangle AOC_{1}}=\frac{1}{12}S
, значит, S_{AB_{1}OC_{1}}=\frac{1}{6}S
. Следовательно, \frac{S_{AB_{1}OC_{1}}}{S_{\triangle ABC}}=\frac{1}{6}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 7.34, с. 67
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.34.1, с. 70

