3459. Две окружности касаются внешним образом в точке K
. Прямая касается первой окружности в точке A
, а второй — в точке B
. Прямая BK
пересекает первую окружность в точке D
, прямая AK
пересекает вторую окружность в точке C
.
а) Докажите, что AD\parallel BC
.
б) Найдите площадь треугольника DKC
, если известно, что радиусы окружностей равны 1 и 4.
Ответ. 3,2.
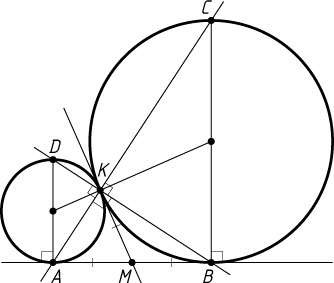
Решение. а) Пусть общая касательная к окружностям, проведённая в точке K
, пересекает отрезок AB
в точке M
(рис. 1). Тогда MA=MK=MB
. Медиана KM
треугольника AKM
равна половине стороны AB
, значит, \angle AKB=90^{\circ}
и \angle BKC=\angle AKD=90^{\circ}
(см. задачу 1188). Значит, AD
и BC
— диаметры окружностей. Тогда AD\perp AB
и BC\perp AB
. Следовательно, AD\parallel BC
.
б) Треугольники ABC
и DBC
равновелики, так как у них одно и то же основание BC
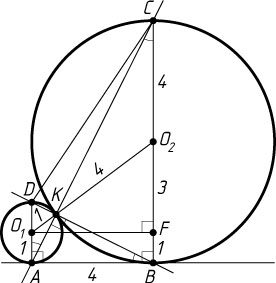
и равные высоты (рис. 2). Следовательно,
S_{\triangle AKB}=S_{\triangle ABC}-S_{\triangle BKC}=S_{\triangle DBC}-S_{\triangle BKC}=S_{\triangle DKC}.
Пусть O_{1}
и O_{2}
— центры окружностей радиуса 1 и 4 соответственно, F
— основание перпендикуляра, опущенного из точки O_{1}
на O_{2}B
. Тогда
BF=O_{1}A=1,~O_{2}F=4-1=3,~AB=O_{1}F=\sqrt{O_{1}O_{2}^{2}-O_{2}F^{2}}=\sqrt{25-9}=4.
Из прямоугольного треугольника ABC
находим, что
AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{16+64}=4\sqrt{5}.
Треугольники AKD
и CKB
подобны с коэффициентом \frac{1}{4}
, поэтому AK=\frac{1}{5}AC=\frac{4\sqrt{5}}{5}
. Треугольник AKB
подобен треугольнику ABC
по двум углам, причём коэффициент подобия равен \frac{AK}{AB}=\frac{\frac{4\sqrt{5}}{5}}{4}=\frac{1}{\sqrt{5}}
. Следовательно,
S_{\triangle DKC}=S_{\triangle AKB}=\left(\frac{1}{\sqrt{5}}\right)^{2}\cdot S_{\triangle ABC}=\frac{1}{5}\cdot\frac{1}{2}AB\cdot BC=\frac{1}{5}\cdot\frac{1}{2}\cdot4\cdot8=\frac{16}{5}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.59, с. 89

