3465. На диагоналях трапеции как на диаметрах построены окружности.
а) Докажите, что их общая хорда перпендикулярна основаниям трапеции.
б) Найдите длину этой хорды, если известно, что основания трапеции равны 1 и 11, а диагонали — 6 и 8.
Ответ. 4,8.
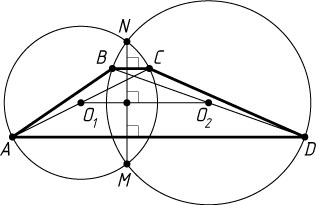
Решение. а) Пусть O_{1}
и O_{2}
— середины диагоналей AC
и BD
трапеции ABCD
с основаниями BC
и AD
(рис. 1). Тогда O_{1}
и O_{1}
— центры окружностей с диаметрами AC
и BD
. Пусть M
и N
— точки пересечения этих окружностей. Линия центров пересекающихся окружностей перпендикулярна их линии центров, поэтому MN\perp O_{1}O_{2}
, а так как отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям, то MN\perp AD
и MN\perp BC
.
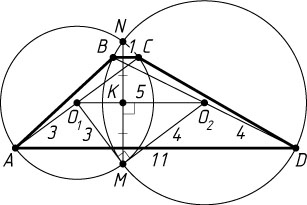
б) Пусть BC=1
, AD=11
, AC=6
, BD=8
(рис. 2). Расстояние между серединами диагоналей трапеции равно полуразности оснований (см. задачу 1226), поэтому
O_{1}O_{2}=\frac{AD-BC}{2}=\frac{11-1}{2}=5.
Линия центров пересекающихся окружностей перпендикулярна общей хорде и делит её пополам, поэтому отрезок MN
вдвое больше высоты MK
треугольника O_{1}MO_{2}
со сторонами O_{1}M=\frac{1}{2}AC=3
, O_{2}M=\frac{1}{2}BD=4
и O_{1}O_{2}=5
. Этот треугольник прямоугольный с прямым углом при вершине M
. Значит,
MK=\frac{O_{1}M\cdot O_{2}M}{O_{1}O_{2}}=\frac{3\cdot4}{5}=\frac{12}{5}.
Следовательно, MN=2MK=\frac{24}{5}=4{,}8
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 10.18, с. 95
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 10.18.1, с. 104

