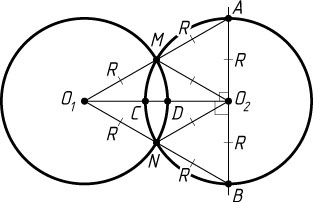
3466. Две равные окружности с центрами O_{1}
и O_{2}
пересекаются в точках M
и N
. Лучи O_{1}M
и O_{1}N
вторично пересекают окружность с центром O_{2}
в точках A
и B
соответственно, причём M
— середина O_{1}A
.
а) Докажите, что точки A
, B
и O_{2}
лежат на одной прямой.
б) Окружности пересекают отрезок O_{1}O_{2}
в точках C
и D
. Найдите отношение отрезка CD
к радиусу окружностей.
Ответ. 2-\sqrt{3}
.
Решение. а) Поскольку каждая из окружностей симметрична относительно прямой O_{1}O_{2}
, точка N
— середина O_{1}B
.
Пусть R
— радиус окружностей. В треугольнике AO_{1}O_{2}
известно, что AM=O_{1}M=O_{2}M=R
, т. е. медиана O_{2}M
равна половине стороны O_{1}A
. Значит, \angle AO_{2}O_{1}=90^{\circ}
(см. задачу 1188). Аналогично \angle BO_{2}O_{1}=90^{\circ}
. Следовательно, точки A
, B
и O_{2}
лежат на одной прямой.
б) Треугольник O_{1}AB
равносторонний, так как AO_{2}=\frac{1}{2}AO_{1}
и
\angle AO_{1}B=2\angle AO_{1}O_{2}=2\cdot30^{\circ}=60^{\circ}.
Поэтому O_{1}O_{2}=\frac{O_{1}A\sqrt{3}}{2}=R\sqrt{3}
. Предположим, что точка C
лежит между O_{1}
и D
. Тогда O_{1}O_{2}=O_{1}D+O_{2}C-CD
, поэтому R\sqrt{3}=R+R-CD
. Отсюда находим, что CD=R(2-\sqrt{3})
. Следовательно, \frac{CD}{R}=2-\sqrt{3}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 10.19, с. 95
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 10.19.1, с. 104
