3469. Дан выпуклый четырёхугольник ABCD
со сторонами AB=3
, BC=CD=5
, AD=8
и диагональю AC=7
.
а) Докажите, что около него можно описать окружность.
б) Найдите диагональ BD
.
Ответ. \frac{55}{7}
.
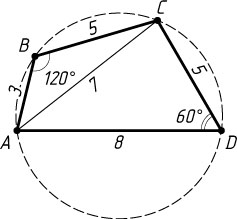
Решение. а) По теореме косинусов (рис. 1)
\cos\angle ABC=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB\cdot BC}=\frac{9+25-49}{2\cdot3\cdot5}=-\frac{1}{2},
\cos\angle ADC=\frac{AD^{2}+DC^{2}-AC^{2}}{2AD\cdot DC}=\frac{64+25-49}{2\cdot8\cdot5}=\frac{1}{2},
значит, \angle ABC=120^{\circ}
и \angle ADC=60^{\circ}
. Сумма противоположных углов четырёхугольника равна 120^{\circ}+60^{\circ}=180^{\circ}
, следовательно, около него можно описать окружность.
б)
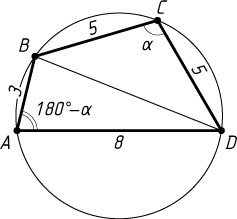
Первый способ. Обозначим, \angle BCD=\alpha
(рис. 2). Тогда по свойству вписанного четырёхугольника \angle BAD=180^{\circ}-\alpha
. По теореме косинусов
BD^{2}=BC^{2}+CD^{2}-2BC\cdot CD\cos\alpha=25+25-2\cdot5\cdot5\cdot\cos\alpha=50-50\cos\alpha,
BD^{2}=AB^{2}+AD^{2}-2AB\cdot AD\cos(180^{\circ}-\alpha)=9+64+2\cdot3\cdot8\cdot\cos\alpha=73+48\cos\alpha.
Из равенства 50-50\cos\alpha=73+48\cos\alpha
находим, что \cos\alpha=-\frac{23}{98}
. Следовательно,
BD=\sqrt{BC^{2}+CD^{2}-2BC\cdot CD\cos\alpha}=\sqrt{50+50\cdot\frac{23}{98}}=\frac{5}{7}\sqrt{98+23}=\frac{5}{7}\cdot11=\frac{55}{7}.
Второй способ. Пусть диагонали AC
и BD
пересекаются в точке K
. Вписанные углы BAC
и DAC
опираются на равные хорды, значит,
\angle CBK=\angle CBD=\angle DAC=\angle BAC.
Тогда треугольники BKC
и ABC
подобны по двум углам (угол при вершине C
— общий), поэтому \frac{BK}{AB}=\frac{BC}{AC}
. Отсюда находим, что
BK=\frac{AB\cdot BC}{AC}=\frac{3\cdot5}{7}=\frac{15}{7}.
Аналогично, из подобия треугольников DKC
и ADC
находим, что DK=\frac{40}{7}
. Следовательно,
BD=BK+DK=\frac{15}{7}+\frac{40}{7}=\frac{55}{7}.
Третий способ. Обозначим \angle BAC=\angle DAC=\alpha
. По теореме косинусов из треугольника ABC
находим, что
\cos\alpha=\frac{9+49-25}{2\cdot3\cdot7}=\frac{11}{14}.
Тогда
\cos\angle BAD=\cos2\alpha=2\cos^{2}\alpha-1=2\cdot\frac{121}{196}-1=\frac{121}{98}-1=\frac{23}{98},
\cos\angle BCD=\cos(180^{\circ}-\angle BAD)=-\cos\angle BAD=-\frac{23}{98}.
Следовательно,
BD=\sqrt{CB^{2}+CD^{2}-2CB\cdot CD\cos\angle BCD}=
=\sqrt{25+25+2\cdot5\cdot5\cdot\frac{23}{98}}=5\sqrt{2+\frac{23}{49}}=5\sqrt{\frac{121}{49}}=\frac{55}{7}.
Четвёртый способ. По теореме Птолемея для вписанного четырёхугольника ABCD
(см. задачу 130) получаем, что
AB\cdot CD+BC\cdot AD=AC\cdot BD,~\mbox{или}~3\cdot5+5\cdot8=7BD,
откуда BD=\frac{55}{7}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 11.47, с. 109
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.47.1, с. 119
Источник: ЕГЭ. — 2018, досрочный экзамен, резервный день 11 апреля

