3475. Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.
Ответ. 5.
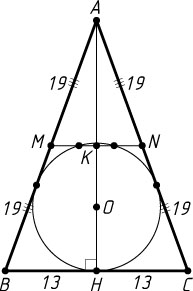
Решение. а) Пусть O
— центр окружности, вписанной в треугольник ABC
со сторонами AB=AC=38
, BC=26
(рис. 1), AH
— высота треугольника, точки M
и N
— середины сторон AB
и AC
соответственно, K
— точка пересечения AH
и MN
, p
— полупериметр треугольника ABC
. Поскольку MN
— средняя линия равнобедренного треугольника, точка K
— общая середина MN
и AH
.
Из прямоугольного треугольника ABH
находим, что
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{38^{2}-13^{2}}=5\sqrt{51},
значит, KH=\frac{1}{2}AH=\frac{5\sqrt{51}}{2}
.
Пусть r
— радиус вписанной окружности треугольника ABC
. Тогда
r=\frac{S_{\triangle ABC}}{p}=\frac{\frac{1}{2}BC\cdot AH}{AB+BH}=\frac{13\cdot5\sqrt{51}}{38+13}=\frac{65\sqrt{51}}{51},
а диаметр вписанной окружности равен 2r=\frac{130\sqrt{51}}{51}
. Поскольку
\frac{130\sqrt{51}}{51}\gt\frac{5\sqrt{51}}{2}~\Leftrightarrow~\frac{130}{51}\gt\frac{5}{2}~\Leftrightarrow~260\gt255,
диаметр окружности больше KH
. Следовательно, вписанная окружность пересекает среднюю линию MN
треугольника.
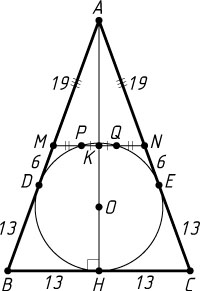
б) Пусть вписанная окружность касается сторон AB
и AC
в точках D
и E
соответственно (рис. 2), а средняя линия MN
пересекает эту окружность в точках P
и Q
(P
между M
и Q
). Тогда
AD=p-BC=51-26=25,~MD=AD-AM=25-19=6
(см. задачу 219). По теореме о касательной и секущей MD^{2}=MP\cdot MQ
, а так как
MP=NQ=\frac{1}{2}(MN-PQ)=\frac{1}{2}(13-PQ),
MQ=MP+PQ=\frac{1}{2}(MN+PQ)=\frac{1}{2}(13+PQ),
то 36=\frac{1}{4}(13-PQ)(13+PQ)
. Отсюда находим, что PQ=5
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.42, с. 119
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.41.1, с. 129
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015

