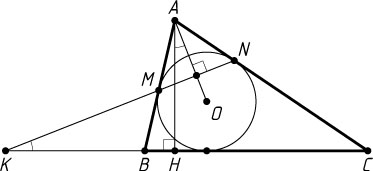
3478. Окружность с центром O
, вписанная в треугольник ABC
, касается сторон AB
и AC
в точках M
и N
соответственно, AH
— высота треугольника. Прямые MN
и BC
пересекаются в точке K
.
а) Докажите, что \angle MKB=\angle OAH
.
б) Найдите AK
, если известно, что \angle ABC=77^{\circ}
, \angle ACB=17^{\circ}
, а отрезок, соединяющий точку H
с серединой MN
, равен 8.
Ответ. 16.
Решение. а) Поскольку AH\perp BC
и AO\perp MN
(рис. 1), углы MKB
и OAH
равны как углы с соответственно перпендикулярными сторонами.
б) Пусть P
— точка пересечения MN
и AO
(рис. 2). Тогда \angle APK=\angle AHK=90^{\circ}
. Из точек P
и H
отрезок AK
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AK
. Угол между высотой и биссектрисой треугольника, проведёнными из одной вершины, равен модулю полуразности двух других углов треугольника (см. задачу 1106), поэтому
\angle PAH=\frac{1}{2}(77^{\circ}-17^{\circ})=30^{\circ}.
По теореме синусов
AK=\frac{PH}{\sin\angle PAH}=\frac{8}{\sin30^{\circ}}=16.

Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 13.47, с. 131
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 13.47.1, с. 142

