3481. AA_{1}
, BB_{1}
и CC_{1}
— высоты остроугольного треугольника ABC
с углом 45^{\circ}
при вершине C
.
а) Докажите, что треугольник A_{1}B_{1}C_{1}
прямоугольный.
б) Найдите отношение, в котором высота AA_{1}
делит отрезок B_{1}C_{1}
, если известно, BC=2B_{1}C_{1}
.
Ответ. 2:1
, считая от точки B_{1}
.
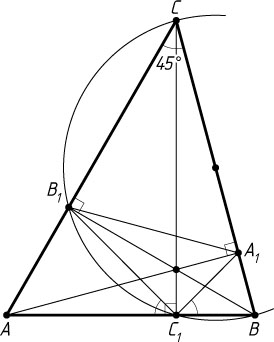
Решение. а) Из точек B_{1}
и C_{1}
отрезок BC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BC
(рис. 1). Поэтому
\angle AC_{1}B_{1}=180^{\circ}-\angle BC_{1}B_{1}=\angle BCB_{1}=45^{\circ}.
Аналогично \angle BC_{1}A_{1}=45^{\circ}
. Следовательно,
\angle B_{1}C_{1}A_{1}=180^{\circ}-\angle AC_{1}B_{1}-\angle BC_{1}A_{1}=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}.
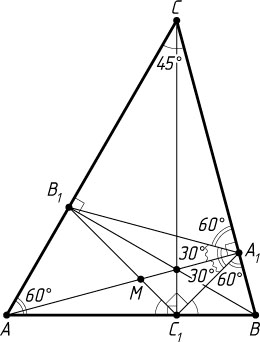
б) Поскольку \angle AC_{1}B_{1}=\angle ACB
, треугольник AB_{1}C_{1}
подобен треугольнику ABC
по двум углам (рис. 2), причём коэффициент подобия k
равен \frac{B_{1}C_{1}}{BC}=\frac{1}{2}
. Значит,
\cos\angle BAC=\cos\angle BAB_{1}=\frac{AB_{1}}{AB}=k=\frac{1}{2}
(см. задачу 19). Значит, \angle BAC=60^{\circ}
. Тогда \angle CA_{1}B_{1}=60^{\circ}
и \angle BA_{1}C_{1}=60^{\circ}
. Значит,
\angle B_{1}A_{1}C_{1}=180^{\circ}-2\cdot60^{\circ}=60^{\circ},~\angle AA_{1}B_{1}=90^{\circ}-60^{\circ}=30^{\circ},
поэтому A_{1}A
— биссектриса угла B_{1}A_{1}C_{1}
.
Пусть M
— точка пересечения высоты AA_{1}
с отрезком B_{1}C_{1}
. Тогда A_{1}M
— биссектриса прямоугольного треугольника A_{1}B_{1}C_{1}
, а так как острый угол A_{1}B_{1}C_{1}
этого треугольника равен 30^{\circ}
, то A_{1}B_{1}=2A_{1}C_{1}
. Следовательно, по свойству биссектрисы треугольника
\frac{B_{1}M}{MC_{1}}=\frac{A_{1}B_{1}}{A_{1}C_{1}}=2.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 15.27, с. 151
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 15.26.1, с. 162

